Mensuration – Measurement

2 Dimensional Shapes

• Important tips
  • There is no volume of 2d Shapes in our syllabus
  • Remember, 3d shapes will ALWAYS have a volume and surface area
  • Remember
    • Perimeter is always with 1 exponential power. So, cm, m, mm etc.
    • Area always has a square in it so cm², mm², m², km² etc.
    • Volume always has a cube power, so cm³,m³,mm³, km³ etc.
  • Try to understand the concept with perimeter and surface area to make sure you attempt the questions correctly
    • In 2d shapes, what we are doing is adding all the boundaries of any shape to find the perimeter
      • Keep this is mind when you are doing complex shapes

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

• • • • • In 3d shapes
          • We are adding the area of every OUTWARDLY visible 2d surface’s area of the overall 3d shape to find surface area.
          • This thinking will help a lot when you find surface area of overall stuff.
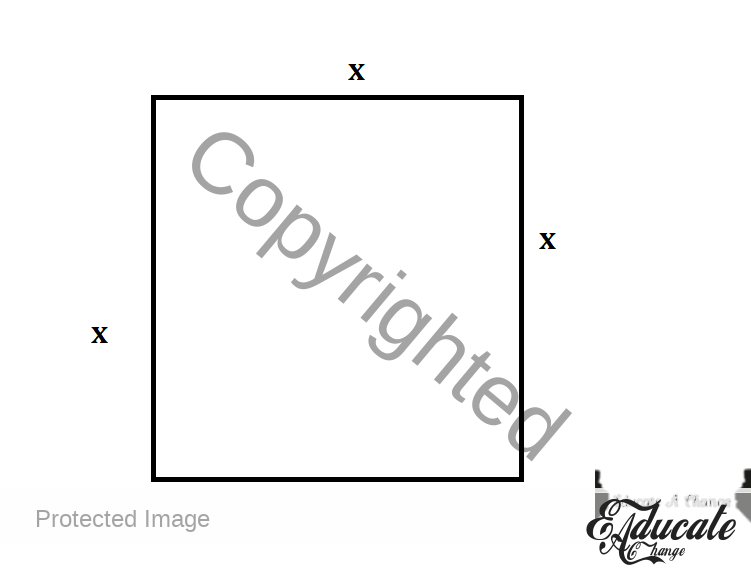
        • Square
          • Area
            • x * x
            • OR x²
            • Where x is ANY Length
              • Why?
              • All lengths are the same
                • Important point for paper 1
              • Perimeter
                • 4x
                • OR 4 multiplied by the length of any side

• Rectangle
  • Area
    • l * b
    • length x breadth
    • length and breadth must be different
    • If both same
      • It will be a square
    • Perimeter
      • 2l + 2 b
      • Just add the 4 sides

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

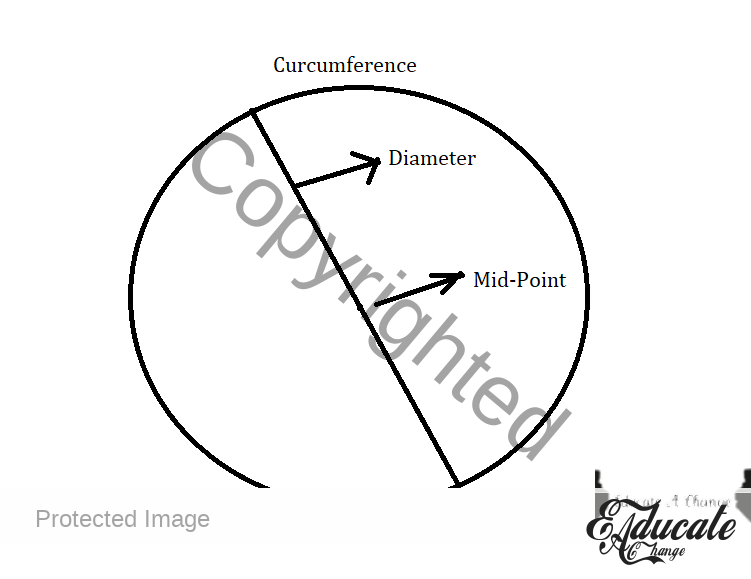
• Circle
  • A complete circle
    • Area
      • πr²
      • Pi is not totally equal to 3.142
        • Instead, pi is an endless number, remember that for paper 1 conceptual part.
        • It is an irrational number
      • Circumference (perimeter of the circle is also called its circumference
        • 2πr

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

• A half circle called a semi-circle
  • Area
    • πr²/2
  • Circumference
    • πr
  • Remember, radius is diameter divided by 2

• A quarter circle
  • Area
    • πr²/4
  • Circumference
    • πr/2
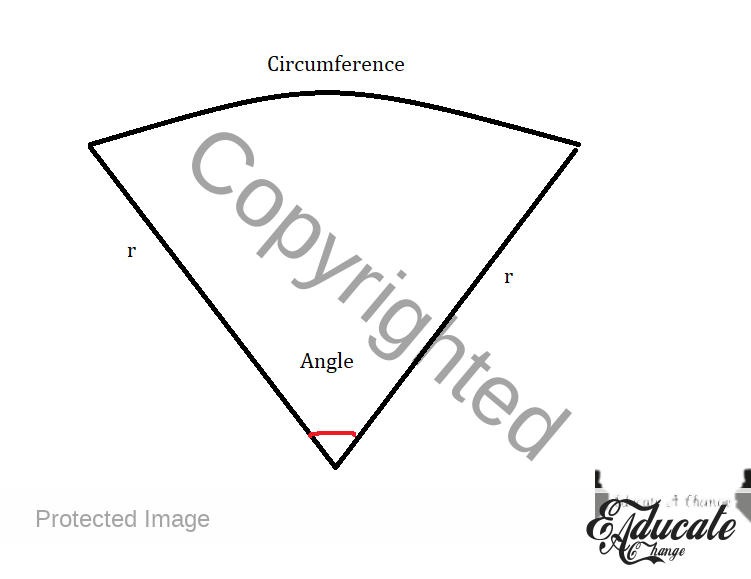
  • A sector of a circle
    • 
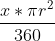
    • Where x is the number of degrees of the sector
  • Circumference of the sector
    • 

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

• Triangle
  • Area of right angled triangle
    • 5 * b * h
    • b = base
    • h = perpendicular height or the height that makes an angle of 90 degree with the base
  • Remember, it will only be a right angled triangle if there is a 90 degree angle given.

• Perimeter
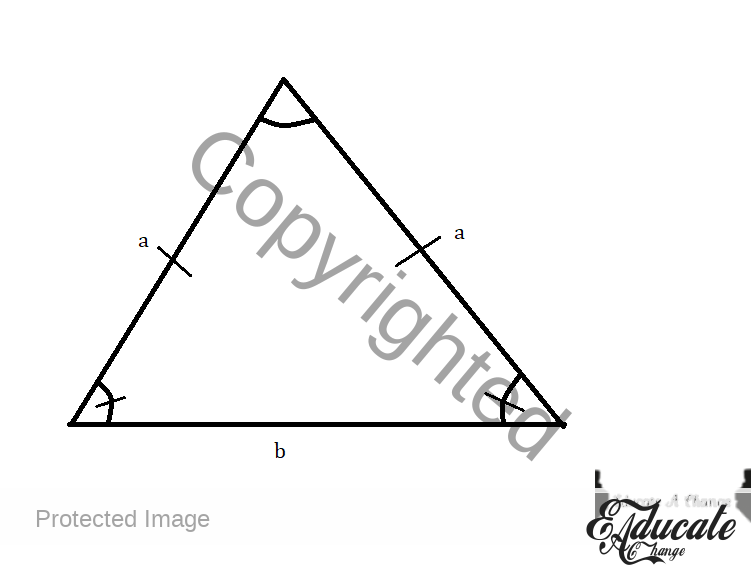
  • Add the length of all three sides if scalene triangle
  • If isosceles triangle
    • Uncommon side + 2 (common side)
    • Here, in the picture, both a have same angles and side length

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

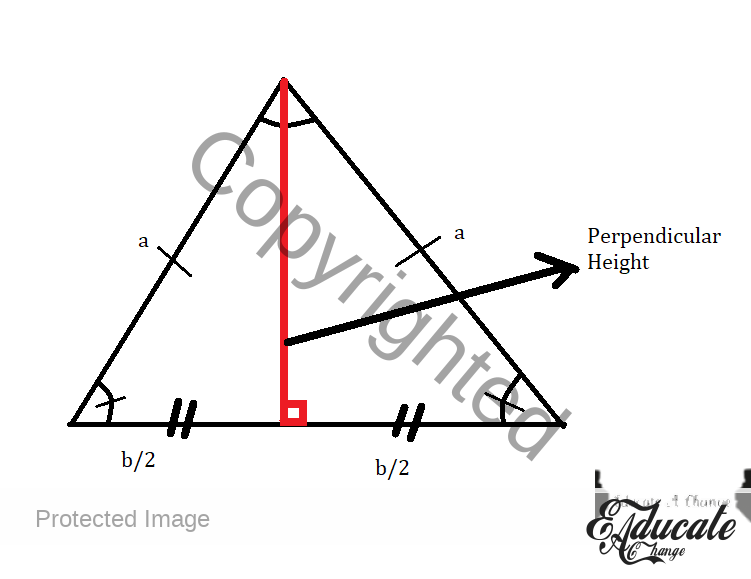
• You can also convert an isosceles triangle to 2 right angled triangle by cutting it in half for the UNCOMMON SIDE.

• If right angled triangle
  • Base + Perpendicular Height + Slant Height
• Equilateral triangle
  • 3 * length of any one side
  • All sides are equal
• How to find slant height in right angled
  • Pythagoras Theorem
    • hypotenuse or slant height² =  base² + perpendicular height²
    • So
      • Perpendicular height = √(hypotenuse² – base²)
      • Base = √(hypotenuse² – perpendicular height²)
      • Remember
        • When we remove square from any side, we take a square root on the complete other side.
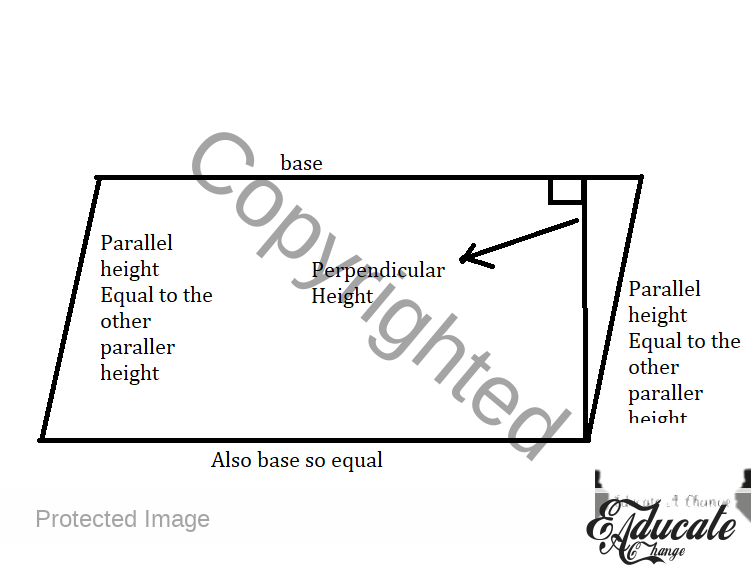
      • Parallelogram
        • Area
          • base * perpendicular height
            • Remember
              • It is not the diagonal height
              • Instead, it is the perpendicular height
            • Perimeter
              • 2(base) + 2 (diagonal Length)
                • NOT THE PERPENDICULAR HEIGHT

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

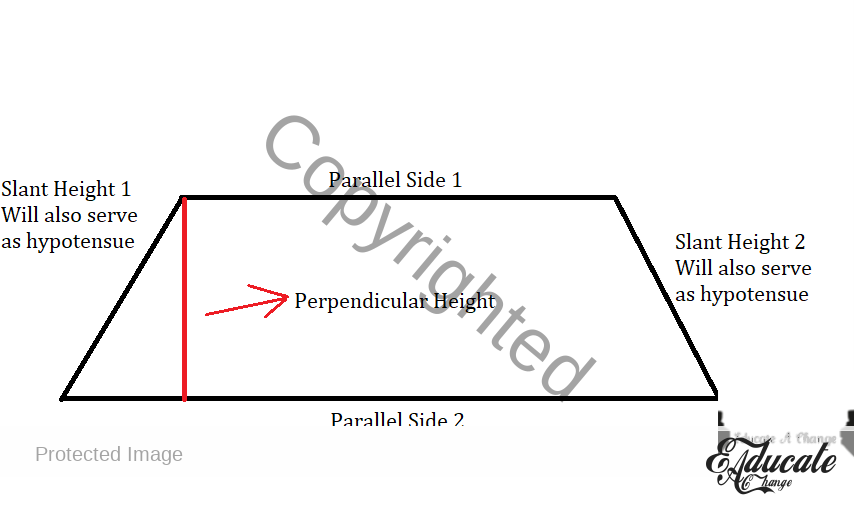
• Trapezium
  • Area
    • 5 * height (PERPENDICULAR HEIGHT) * (sum of parallel sides)
    • 5 * h * (parallel side 1 + parallel side 2)
    • Remember
      • If parallel sides had equal length, it would have been a parallelogram
    • Perimeter
      • Parallel side 1 + parallel side 2 + slant height 1 + slant height 2

3D Shapes

• Cube
  • Volume
    • l³
    • All lengths are the same
  • Surface Area
    • 6l²

• Now lets try to understand what is happening in surface area

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

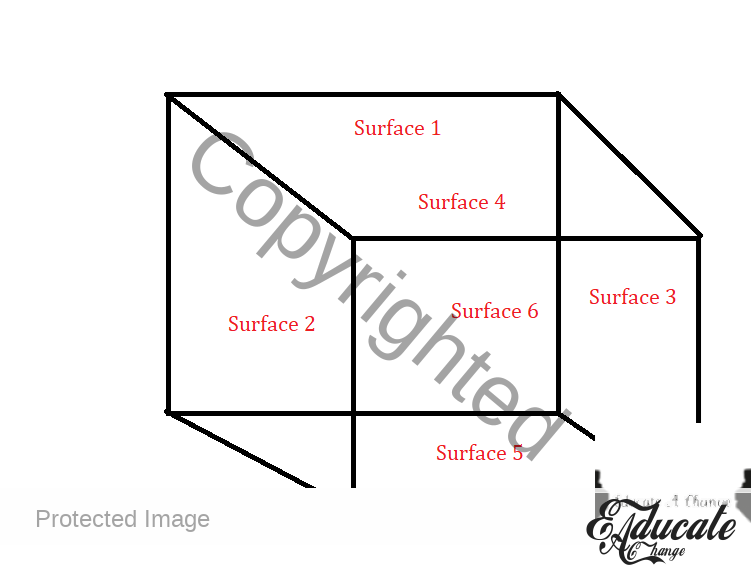
• Here are 6 surfaces that are all SQUARES
• We are just finding the areas of 6 squares to find the surface area of the entire shape
  • One square has a area of l²
  • So 6 surfaces of equal sqaure
    • 6l²
  • Cuboid
    • Volume
      • l * b * h
      • Length x breadth x height
    • Surface area
      • 2(l * b) + 2 (l * h) + 2 (b*h)
    • Now the common scenario is that of an open cuboid

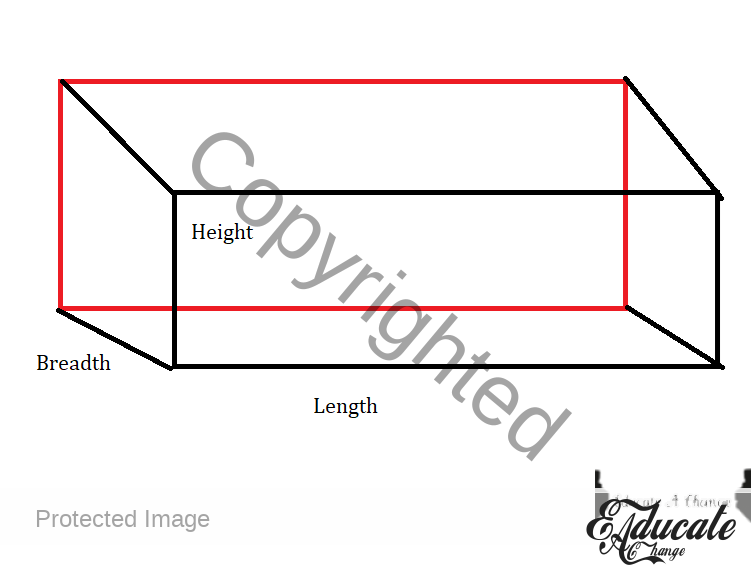
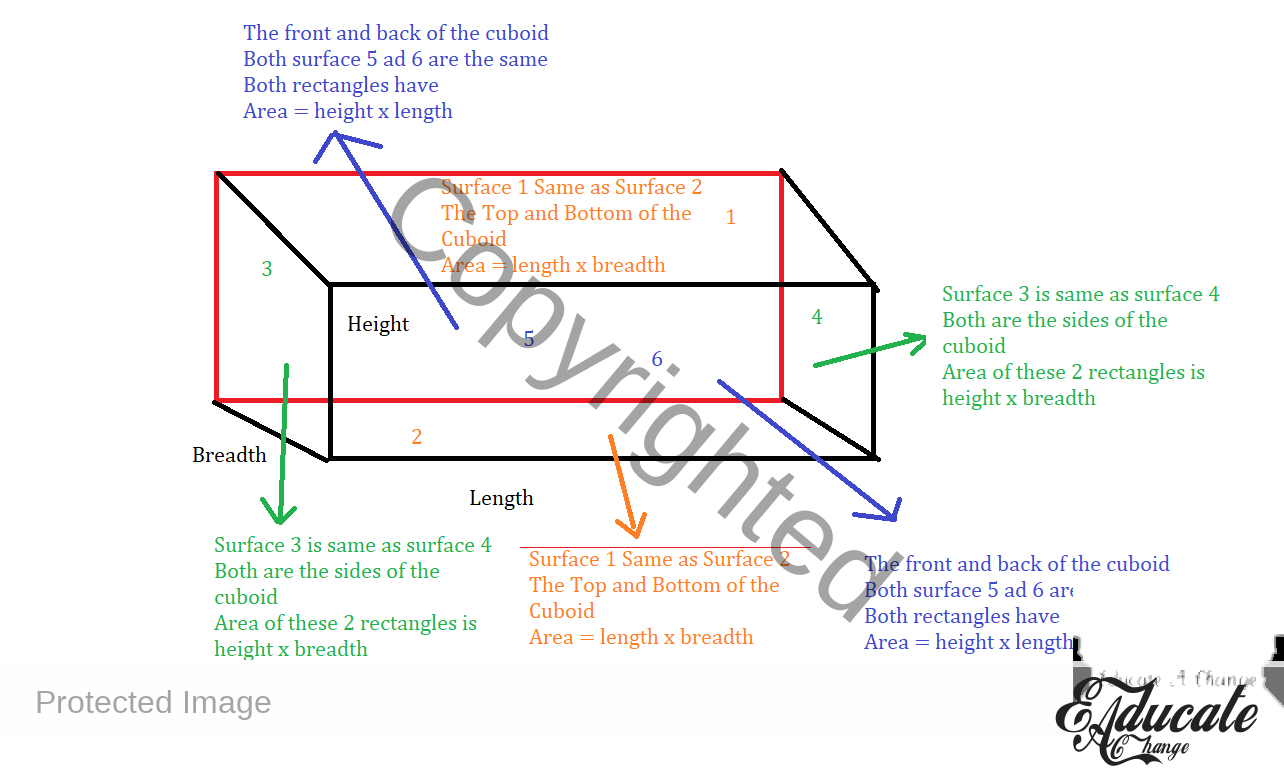
• Now let us understand what is happening in surface area
  • 6 surfaces.
  • There are 2 surfaces that have the same area based on measurements
    • Remember, each surface is a rectangle
    • We are finding the area of 6 rectangles and adding them together to find the overall surface area of the cuboid

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

• Remember, open cuboid basically has ONE surface missing out of the total 6 surfaces that we add in the normal surface area. So just take out that one surface. Simple!
• Let us try a few examples
  • Let us say that there is an open WATER tank for which you have to find the surface area.
    • It means that the TOP surface s not present
    • We still have 2(length x height) which are the front and back
    • We still have the 2 (breadth x height) which are the side surfaces
    • We ONLY HAVE ONE of the two surfaces from top and bottom, because the top (the tank’s top) has been removed so we don’t have 2(length  x breadth).
      • Instead, we only have length x breadth
      • Which is just one of the two surfaces.
    • So our total equation becomes
      • 2 (length x height + breadth x height) + (length x breadth)
    • That is how to think about it.
  • Sphere
    • Volume
      • 
    • Surface area
      • 4πr²
      • So
        • Curved Surface area of hemisphere is 2πr²
        • Curved Surface area of quarter sphere is πr²
      • HOWEVER
        • When you cute a sphere is half, there is another surface as well i.e. the circle that forms at the bottom
        • DON’T FORGET TO ADD THAT AREA AS WELL

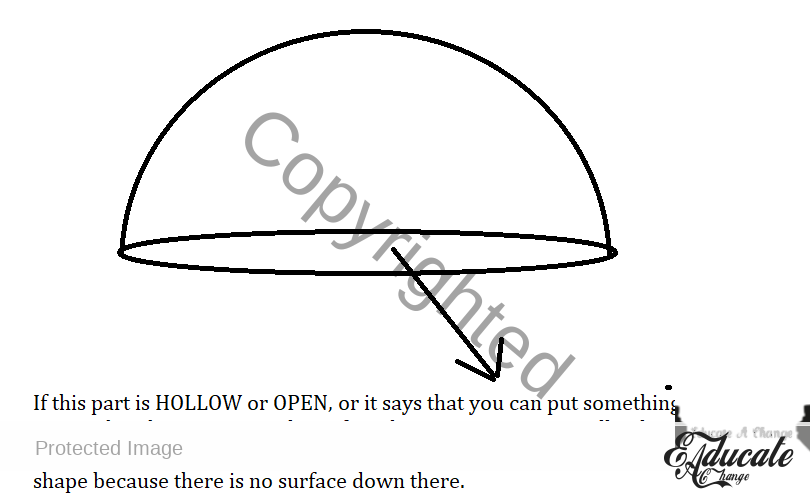
• In the above case, we will ONLY take the curved surface area because the bottom extra circle does not exist. So it will be 2πr²

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

• Here, as there are two surface, we need to add the hemisphere that is 2πr² and an additional circle for the base which is πr² so the total surface area of this shape will be 3πr²

• Cone
  • Cone has 2 height
    • One if the perpendicular height from the top-most thin part to the center of the bottom
    • The other one is the slant height
  • Volume of cone
    • (πr²h)/3
  • Surface area of come
    • If the come has nothing at its bottom, i.e. it is a hollow come
    • Then
      • πrl
        • Where l is the slant height
      • If the below part is visible, then there is a circle as well
        • Add that circle so
        • Area of circle is πr²
        • Area of curved cone is
        • πr l
        • So total area of a curved cone with bottom part visible
          • πr² + πrl
        • So, if we have an open cone

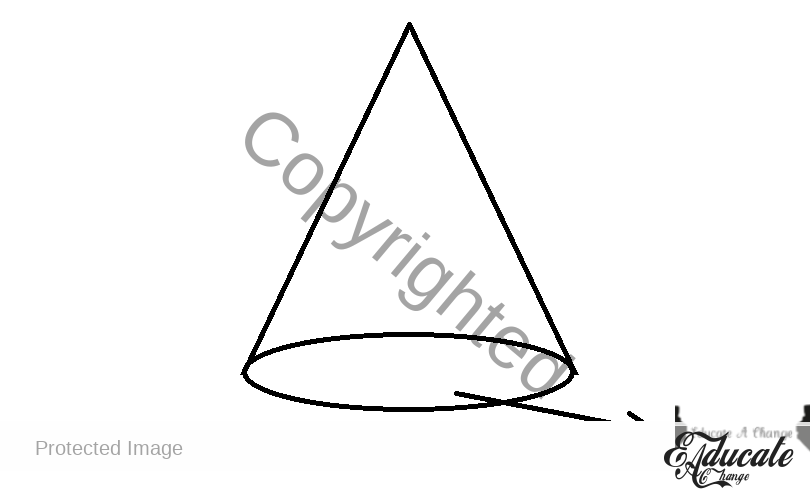
• Here, as the circular surface below is completely OPEN, we do not have a base. So we will only take the surface area of the curved part of the cone.  So we will take πrl

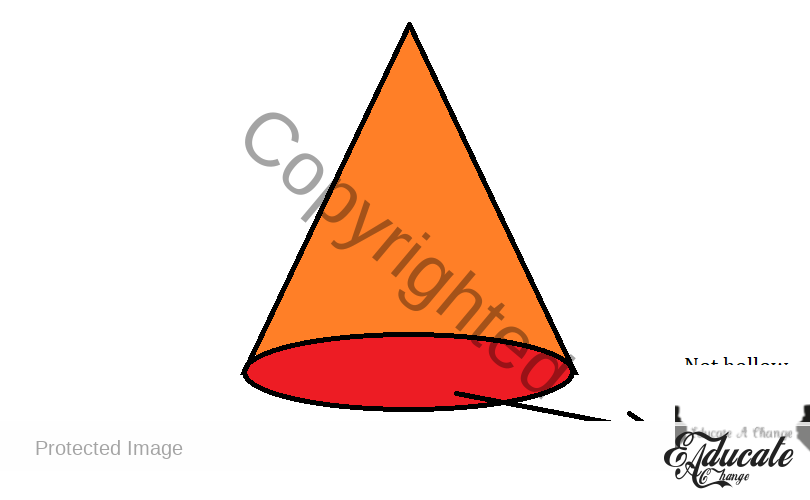
• Here, we have two surfaces. One closed surface, which is the closed circle at the bottom which we can touch, which is an area of πr²
• The second is the curved surface which is  πrl
• So the total becomes πr² + πrl
• Again, thinking correctly is the way forward.

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

• Cylinder and Prism
  • Remember, a cylinder is a type of prism. What is a prism?
    • Basically ANY SHAPE that when you cut from any part in the middle or take a CROSS-SECTION, it will be the same shape with reduced length.
      • For example, on type of prism is a breadloaf
      • The second type is a triangular prism

• So for ANY prism
  • The volume is equal to
    • base area (the area of the base surface) x height / length
  • So for this triangular prism
    • The volume will be
      • 5 * b * h (base area of the triangle as the base / cross-section) * total length of the shape  (we will take complete base because isosceles triangle
        • IF we have right angled, same formula but base will be different.
      • So

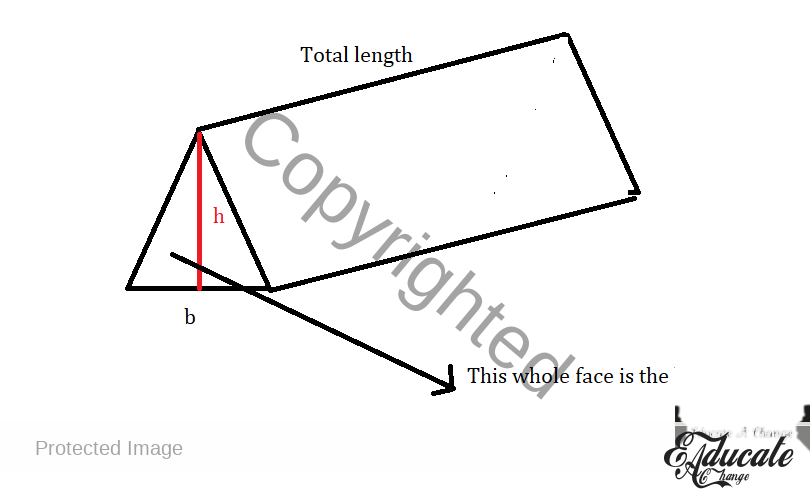
• Surface area
  • The area of all the 2d surfaces that are NOT hollow added together. REMEMBER THIS TRICK
  • So for the shape above
    • If both the ends are closed, there are 2 triangles so the area of those two triangles, plus the 3 sides.
    • Now the issue gets more complicated if the triangle is isosceles. Try thinking of each surface so

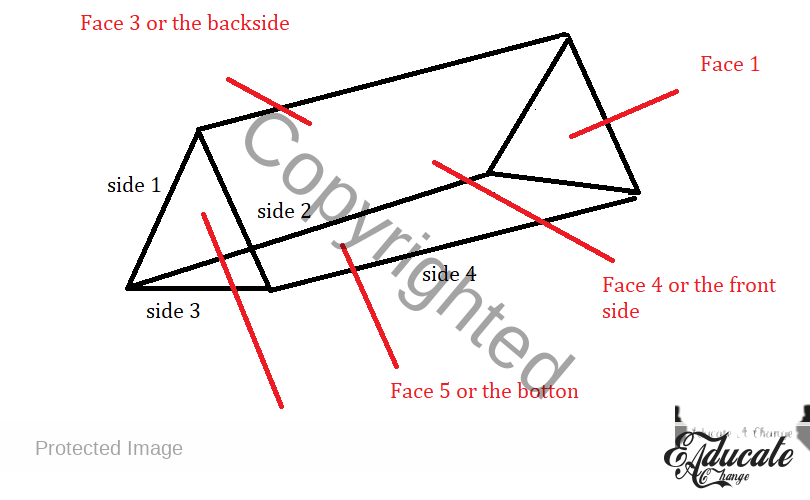
• Face 1 is a triangle so area will be 0.5 * base * height (taking complete base as isosceles triangle
• Face 2 is another triangle, we will add to face 1 the same calculation once again

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

• Face 3 is a rectangle with base the same length as side 4 and height side 1
  • So we have side 4 * side 1 for its area
• Face 4 is a rectangle with length side 4 and breadth side 2
  • So side 4 * side 2
• Face 5 is a rectangle as well with breadth side 3 and length side 4
  • So side 3 * side 4
• The total surface area is Face 1 + Face 2 + Face 3 + Face 4 + Face 4
  • As single as this.
• Now let us consider a cylinder
  • A cylinder is a prism with a circular base.
    • Volume is base area * height
      • So πr²h

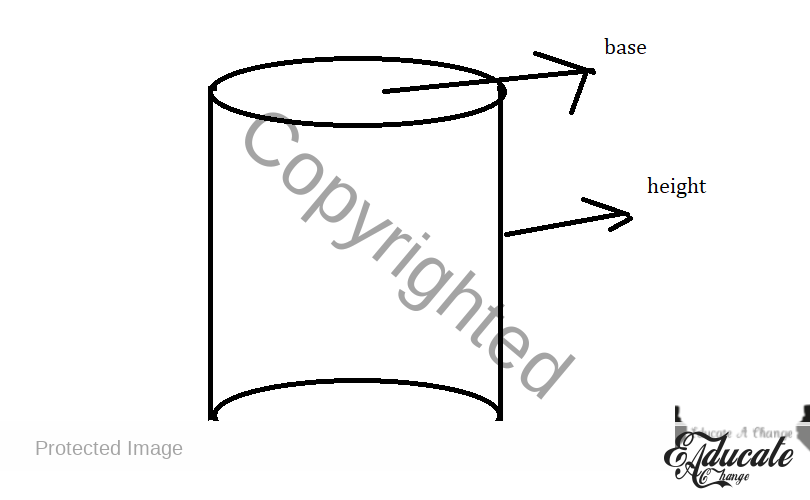
• Surface Area
  • IF, both sides are open
    • Then only the curved surface area
      • 2 πrh
    • If one side is a closed surface and we can touch it, means a circle adds to it
      • So πr² for the circular base
      • and 2πrh for the curved part
      • Can also write as πr(2h + r)
    • If both sides are closed, and we can touch both surfaces, there are 2 circles.
      • πr² for one circle
      • πr² for another circle
      • 2πrh for the curved part
      • Or
        • 2 πr (r+h)

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

Now – let us consider a few ways the examiner tricks you

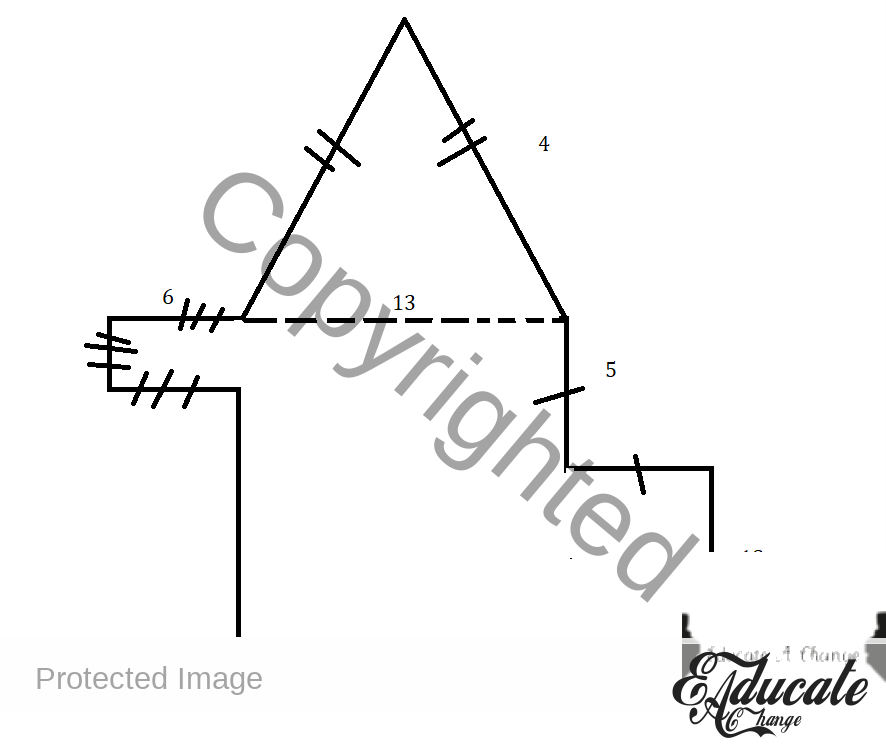
• If you are asked to find the perimeter of this shape
• First identify the sides you need to add REMEMBER perimeter is adding all the outside sides NOT THE INSIDE ones.

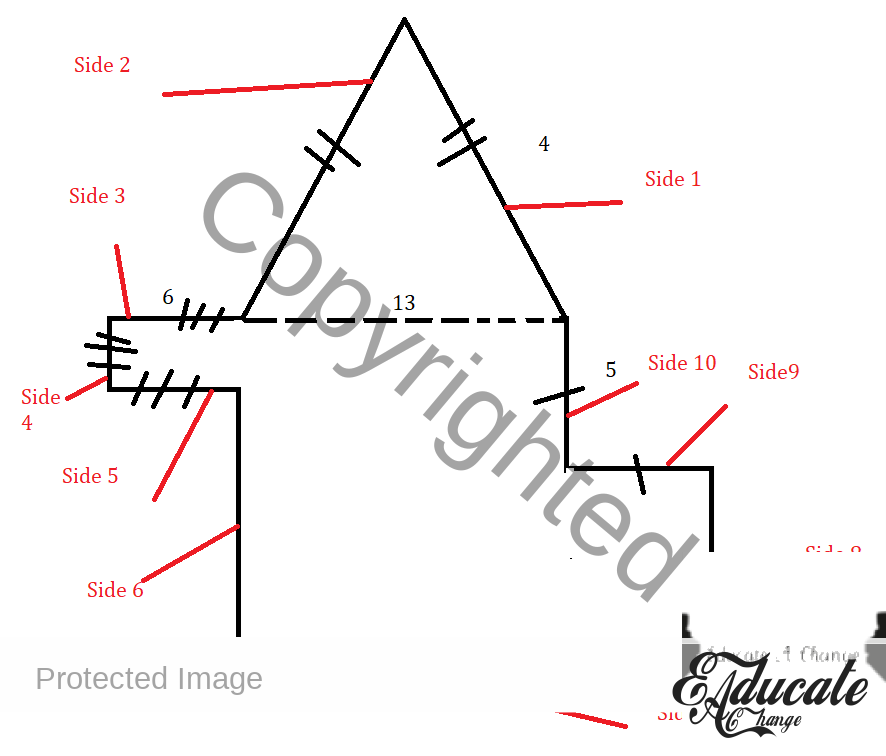
• Now let us just add each side
• Side 1 is 4 cm
• Side 2 is same as side 1 so 4 cm
• Side 3 is 6 cm
• Side 4 is same as side 3 so 6 cm
• Side 5 is also same as side 3 so 6 cm
• Side 6 is 18+5 – 6 = 17
• Side 7 is 13 + 5 = 18
• Side 8 is 18
• Side 9 is 5 cm
• Side 10 is 5 cm
• So total perimeter is
  • 89 cm
• For area however,
  • you will divide the inside shapes individually, find the area of each sub shape and add it together.

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |

Now a tricky one for surface area

• A hollow cylinder from one side with a hemisphere on the other side

• • In this case, for surface area
    • Only the curved area of cylinder and the hemisphere’s curve area will be taken, because no other touchable base exists on the outside.
    • So
      • 2 πrh for cylinder curved area PLUS
      • 2 πr² for the curved hemisphere
      • Add them
      • Formula made on spot

Content by Educate A Change (by Hunain Zia) | Copyrighted by AYLOTI | Redistribution, download, sharing, selling or any form of unauthorized use of data is strictly prohibited |