Paper 2: Logic Gates and Truth Table | O Level Computer Science 2210 & IGCSE Computer Science 0478 | Detailed Free Notes To Score An A Star (A*)
- Role of logic gates
- The computer can only understand 0 and 1.
- As a result, logic gates determine information based on 0 and 1.
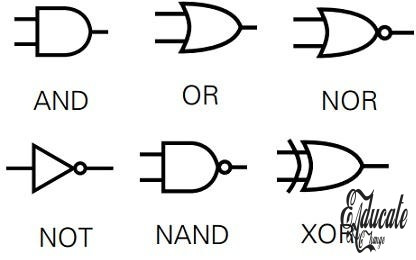
- Main Gates
- AND
- 2 inputs
- Both need to be 1 to give 1 as the answer
- Otherwise, in any other case, would be 0
- NOT gate
- Only 1 input
- It would reverse the input
- Make 0 into 1 and 1 into 0
- OR
- 2 inputs
- Both inputs 1 so 1
- Any one of the input 1 then 1.
- Both inputs 0 then 0
- NAND
- 2 Inputs
- AND + NOT
- Reverses output of AND
- Therefore, two inputs
- Both 1 then 0
- In all other cases, it will be 1.
- NOR
- 2 inputs
- It is OR plus NOT gate
- Therefore, it reverses the output of NOT gate
- If both zero than it gives 1 output
- Otherwise, it will give 0 output
- XOR
- The XOR gate focuses on giving a 0 output if both inputs same.
- 2 Inputs
- If both 1 then 0
- If both 0 then 0
- If 1 is 0 and 1 is i1, then output is 1
- AND
- How to write gate equations
- NOT
- We either write NOT A or a small dash over A
- AND
- We either write A AND B
- We can write A.B
- OR
- We can either write A OR B
- We can write A+B
- NAND
- We can either write A.B and a bar on both of them
- OR We can write A NAND B
- NOR
- We can write A+B and a bar on both of them or we can write A NOR B
- XOR
- We can either write A XOR B
- Or we can write A + B and make a round circle around the + sign
- NOT
- When making logic diagrams, remember that a straight line shows the flow of data
- We can use a jerk in the lines to show where there is no connection between the gates.
- How to build the truth table for the logic gates
- For AND
- How to name the variables in the truth table
- If only two, do the following
| A | B |
| 1 | 1 |
| 1 | 0 |
| 0 | 1 |
| 0 | 0 |
- If there are three of them, do the following
| A | B | C |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
- AND Gate
| A | B | AND |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
- OR
| A | B | OR |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
- XOR
| A | B | XOR |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
- NAND
| A | B | NAND |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
- NOR
| A | B | NOR |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
- NOT
| A | NOT |
| 1 | 0 |
| 0 | 1 |
Pictures of Gates (Taken courtesy online)
Please go through the video lecture on how to create the logic circuit and fill out the truth table for difficult logic gates.