Probability | O Level Mathematics 4024 & IGCSE Mathematics 0580 | Detailed Free Notes To Score An A Star (A*)

Basics

• Probability means the chances of something occurring or not occurring.
• These chances can be calculated mathematically.
• Remember
  • In probability, where ever you see the word “AND”, you will multiply. On the other hand, where ever you see the word “OR” you will add.
  • Just memorize this rule, it will make your life a lot easier.
• A simple example: a six-faced dice.
  • When someone throws a dice with 6 faces, there is a 1 in 6 chance that one of the faces will come on the top.
    • In other words
      • There is a 1/6 chance that 1 will come on top
      • There is a 1/6 chance that 2 will come on top
      • There is a 1/6 chance that 3 will come on top
      • There is a 1/6 chance that 4 will come on top
      • There is a 1/6 chance that 5 will come on top
      • There is a 1/6 chance that 6 will come on top
    • However, let us say that the faces of the dice have the following numbers instead of the usual 1,2,3,4,5,6: they have 1,1,1,3,3,5
      • Now when I roll this dice, the chances of 1 coming on the top are based on the fact that either the first face with 1 will come on the top OR the second face with 1 will come on the top OR the third face with 1 will come on the top.
        • Remember, where OR is used, we add.
        • So 1/6 +1/6 +1/6
        • We have a probability of 3/6 that 1 will come on the top.
        • Simplify it to get 1/2
          • So out of the six faced, 3 are marked “1” which means the probability of 1 coming on the top is 3/6.
        • Similarly,
          • The probability of 3 coming on the top with a dice with faces marked 1,1,1,3,3,5 is 2/6 because 2 faces have the number 3 on it. You can simplify it to 1/3.
          • The probability of 5 coming on the top is 1/6 because one face is marked 5.
        • However, in this specific dice with numbers 1,1,1,3,3,5 – the probability coming on the top is 0 because out of the six faces, NONE has the number 6 on it.
      • Now let us take a little complex to understand the “AND” function
        • Let us say you roll two standard dice. Both dice have 1,2,3,4,5,6 marked on each of their faces.
        • What is the probability that I will get a “1” on the first dice AND a “1” on the second dice.
          • Let us break down the problem and think about it.
            • The chances of me getting a 1 on the first dice are 1/6 because only 1 face on the first dice has the number 1 on it.
            • The chances of me getting a 1 on the second dice are 1/6 because only 1 face on the first dice has the number 1 on it.
            • The middle operator here is AND, so I will multiply the first and the second probabilities 1/6 * 1/6 = 1/36
            • Thus, if I roll both standard dice, there is a 1/36 chance that both of them will show number 1 on the top.
          • What would happen if the same question said: what are the chances that you get number “2” on first dice and number “3” on second dice?
            • The answer would be the same
            • Why? Let us break it down
              • The chances of me getting a 2 on the first dice are 1/6 because only 1 face on the first dice has the number 2 on it.
              • The chances of me getting a 3 on the second dice are 1/6 because only 1 face on the first dice has the number 3 on it.
              • The middle operator here is AND, so I will multiply the first and the second probabilities 1/6 * 1/6 = 1/36
              • Thus, if I roll both standard dice, there is a 1/36 chance that the first of them will show number 2 on the top, and the second will show number 3 on the top are 1/36
            • However, the situation would change if he says: what are the chances that you get a 2 and a 3 on roll (throwing both dice).
              • Now the situation is more complex
              • Let us break it down
                • The first scenario: there is a 2 on the first dice and a 3 on the second dice
                  • In this case,
                  • The chances of me getting a 2 on the first dice are 1/6 because only 1 face on the first dice has the number 2 on it.
                  • The chances of me getting a 3 on the second dice are 1/6 because only 1 face on the first dice has the number 3 on it.
                  • The middle operator here is AND, so I will multiply the first and the second probabilities 1/6 * 1/6 = 1/36
                • The second scenario is that there is a 3 on the first dice and a 2 on the second dice
                  • In this case
                  • The chances of me getting a 3 on the first dice are 1/6 because only 1 face on the first dice has the number 3 on it.
                  • The chances of me getting a 2 on the second dice are 1/6 because only 1 face on the first dice has the number 2 on it.
                  • The middle operator here is AND, so I will multiply the first and the second probabilities 1/6 * 1/6 = 1/36
                • Both the first OR the second scenarios will result in one dice showing 3 and the other dice showing 2.
                  • So we add 1/36 and the other 1/36 (from the first and second scenario)
                  • 2/36
                  • Simplify it
                  • 1/18
                • The key to unlocking and solving any probability question is to break down the complex question and first solve each of its smaller parts. Always think in terms of whether AND would occur or OR would occur under common sense and logic in the given scenario.
                • The next set of notes will focus on replacement and no -replacement scenarios

Replacement and No Replacement

• In probability, we generally assume that something when taken out of a pool or group is not replaced for the next round.
  • For example, if there are 10 blue toffees and 10 black toffees in a bag.
  • I take two toffees from the bag, one after another.
  • Let us say the first toffee I picked was a blue toffee. It means that when I will take out the second toffee, due to no replacement, the bag will now have 9 blue toffees and 10 black toffees with the total toffees falling from 20 to 19.
  • Let us say he asks, what is the probability that you pick both blue toffees
  • In this case
    • The probability that during my first pick I get a blue toffee is 10/20 because total toffees are 20 and 10 of them are blue, so I can simplify it to 1/2.
    • However, during my second pick, 1 blue toffee is already less from the bag, so the next toffee being blue has a 9/19 chance because the total toffees in the bag are now only 19 remaining after my first pick.
    • I need BOTH first AND second pick to be blue. So I will multiply both probabilities.
    • My final probability will become
      • 1/2 * 9/19
      • 9/38
    • However, if he said that pick two toffees WITH replacement, what is the probability that you pick two blue toffees.
      • Let us break down the situation.
      • When I pick the first toffee, there are 20 toffees in total and 10 of them are blue toffees. Which means that in my first pick, I have a 10/20 chance of picking a blue toffee.
      • Simplified: 1/2 chance
      • After I picked the first toffee, the total toffee reduced to 19 and there were 9 blue toffees remaining. However, THIS TIME, I replaced the blue toffee that was missing with a new blue toffee i.e. now the total toffees are back to 20 and the blue toffees are back to 10.
      • Now I make my second pick. Again, there are 10 blue toffees and 20 total toffees. As such, my second pick also has a 10/20 chance that it will be a toffee. Simplify it to get a 1/2 chance.
      • Total: First AND Second pick
        • 1/2* 1/2
        • 1/4 chance of getting a blue toffee on the first AND second pick in case of replacement.

The 1- Trick

• The total probability in any case is equal to one. Why?
  • If we look in fractional terms
    • Say there are 6 toffees in the bag that are blue and a total of 6 toffees only. What is the probability that I will pick a blue toffee?
    • 6/6 is the probability with simplifies to 1/1 or simply 1
    • Similarly, say, there are 20 toffees in a bag 5 are green, 6 are blue, 9 are yellow.
    • If I make a pick, I can get a chance of 5/20 green toffees, 6/20 blue toffees and 9/20 yellow toffees.
    • If we add up all these probabilities, we get 20/20 which is 1/1 or 1.
  • Remember, WE DO NOT EXPRESS probabilities in the form of ratios. However, We DO express them in the form of decimals
  • The total probability is always 1.
    • So lets suppose there are 10 chocolates in a bag. 5 are milk chocolates, and the other 5 are dark chocolates.
    • The probability of picking a milk chocolate is 5/10 or 1/2 or 0.5. The probability of picking a dark chocolate is 5/10 or 1/2 or 0.5.
    • However, think of it like this: the total probability is 0.5+0.5 = 1
      • So, if I have one of the probabilities from the two, I can easily find the other by simply subtracting from the first.
    • So if the probability of dark chocolates is 0.5, I can find probability of blue chocolates (given that they are the ONLY other item in the choice) by simply subtracting it from 1.
      • 1-0.5 = 0.5
    • Let us look at another example.
      • Say there are 3 types of animals in the farm, with total 25 animals. There are 15 goats, 5 horses and 5 cows.
      • The probability of picking a goat at random is 15/25 = 3/5 = 0.6
      • The probability of picking a horse is 5/25 = 1/5 = 0.2
      • So the total probability is 1
      • We can find the probability of picking cows by 1 – 0.6 – 0.2 = 0.2 is the probability of picking cows.

Tree Diagram

• Before tree diagrams in particular: we need to understand the difference between independent and dependent events:
  • Independent events are events are events that occur completely free of each other. So the outcome of EVENT A does not effect the outcome of EVENT B.
    • The example we have covered here in this chapter is of independent events.
  • The second case is dependent events.
    • Events where outcome of one event impacts the outcome of the other event.
    • We will cover this in the next post.
  • Mutually exclusive events
    • Events that can not occur at the same time. For example, you can not be a human and a dinosaur at the same time. You can not be dead and alive at the same time etc. We will cover these in future posts.
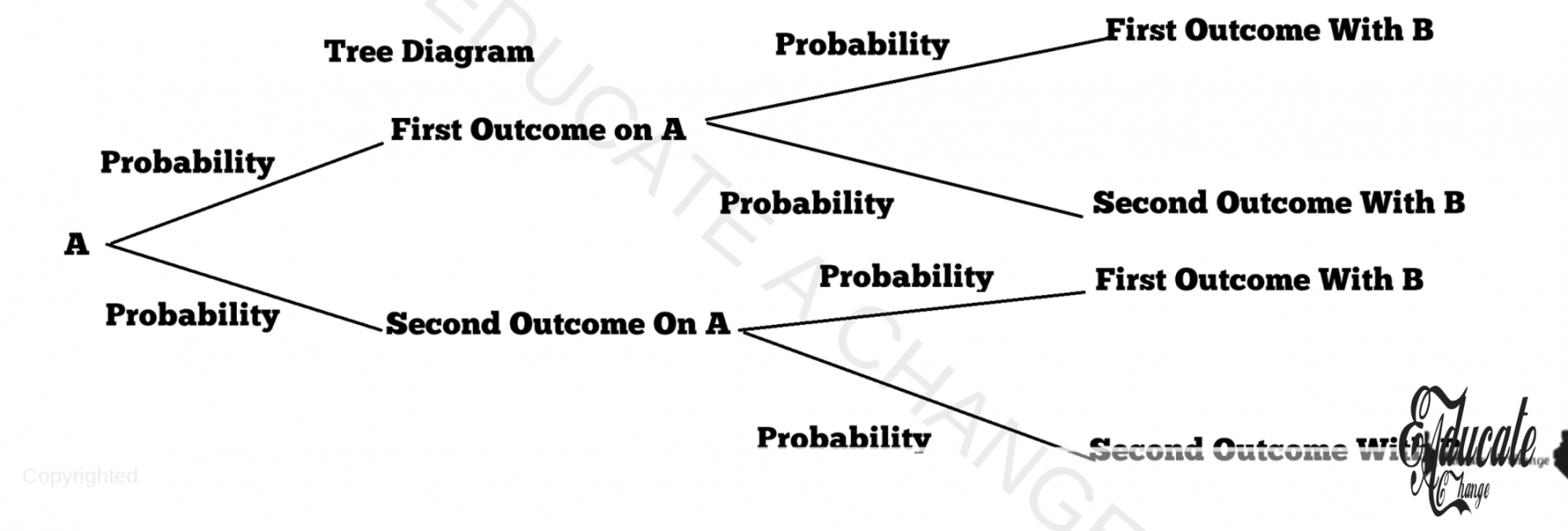
  • The tree diagram using a branched out method to display probabilities of different events.
  • Remember, in our first notes we talked about AND and OR functions. They will be very helpful here.
  • A basic tree diagram is as such
    • Let say there is one main event: A where there are 2 outcomes
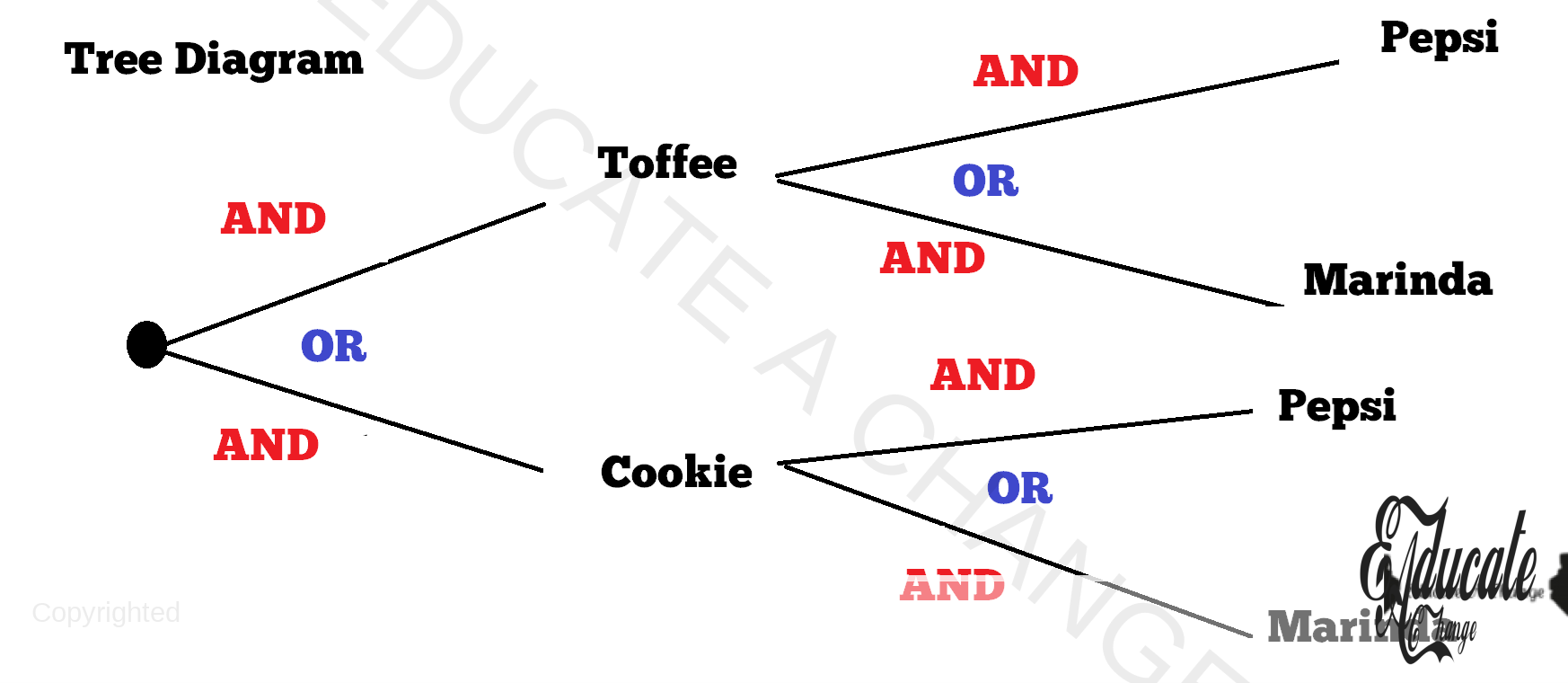
      • For example, there is a bag of candies with 2 types of candies in it: toffees and cookies.
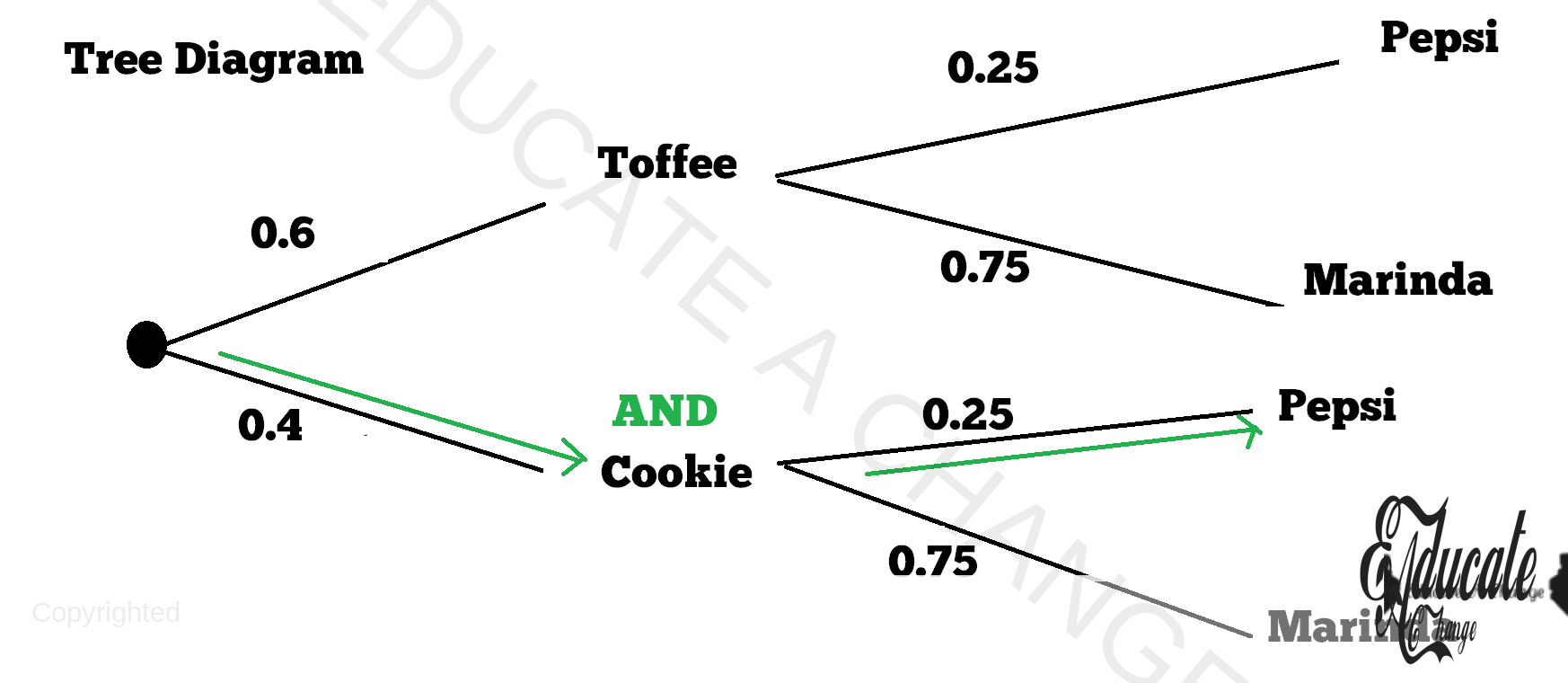
      • I can either select toffee or cookie in my choice of event A. There are a total of 10 candies: 6 are toffees and 4 are cookies and I have to pick randomly.
        • This means we have a 6/10 or 3/5 or 0.6 probability of picking a toffee.
        • This means we have 4/10 or 2/5 or 0.4 probability of picking a cookie.
      • Then, after making selection for event A, I have to further decide event B: the type of drink I want.
        • Let us say there are two outcomes for B: Pepsi or Marinda (yeah I know, but I like it so bear with this example)
        • I can either choose Pepsi or Marinda. There are 20 bottles in the bag. 5 of them are Pepsi and 15 of them are Marinda.
          • The probability that I pick a Pepsi is 5/20 or 1/4 or 0.25.
          • The probability that I pick a Marinda is 15/20 or 3/4 or 0.75.
        • Let us see what a tree diagram would look like:

• Let us break down this diagram: read in detail to avoid the mistakes

1. This one is the name of the first event. You may or MAY NOT write anything here but I suggest that you just leave it blank. Or, in our example, I can simply write here “candies”. But better leave it blank
2. This is the probability of the first outcome. You can take any of the two outcomes to be the first outcome. I select toffees to be the first outcome. Here I will write either 3/5 or 0.6 depending on whether I am using fractions or decimals.
3. This is the probability of the second outcome. My second outcome for candies is cookies. So I will write 0.4 or 2/5 here depending on whether I am using fractions or decimals.
4. This is the name of the first outcome. I will write toffees here.
5. This is the name of the second outcome. I will write cookies here.
6. This is the probability of the first outcome of event B. REMEMBER, DO NOT PERFORM ANY MULTIPLICATIONS OR ADDITIONS AT THIS STAGE. You can select which outcome you wish to keep as the first or second outcome. I will consider the first outcome to be Pepsi. So I will write 0.25 or 1/4 depending on whether I am using fractions or decimals.
7. This is the probability of the second outcome of event b. In my case, it is Marinda, so I will write 3/4 or 0.75 based on whether I am using fractions or decimals.
8. This is the exact same as 6.
9. This is the exact same as 7.
10. This is the name of the first outcome of event B, which in my case is Pepsi.
11. This is the name of the second outcome of even B, which in m case is Marinda.
12. This is the exact same as 10.
13. This is the exact same as 11.

Now, let us see how the tree diagram looks like in fractions and decimals.

For Our Question, A Decimal Tree Diagram Will Look Like

For Our Question, A Fractional Tree Diagram Will Look Like

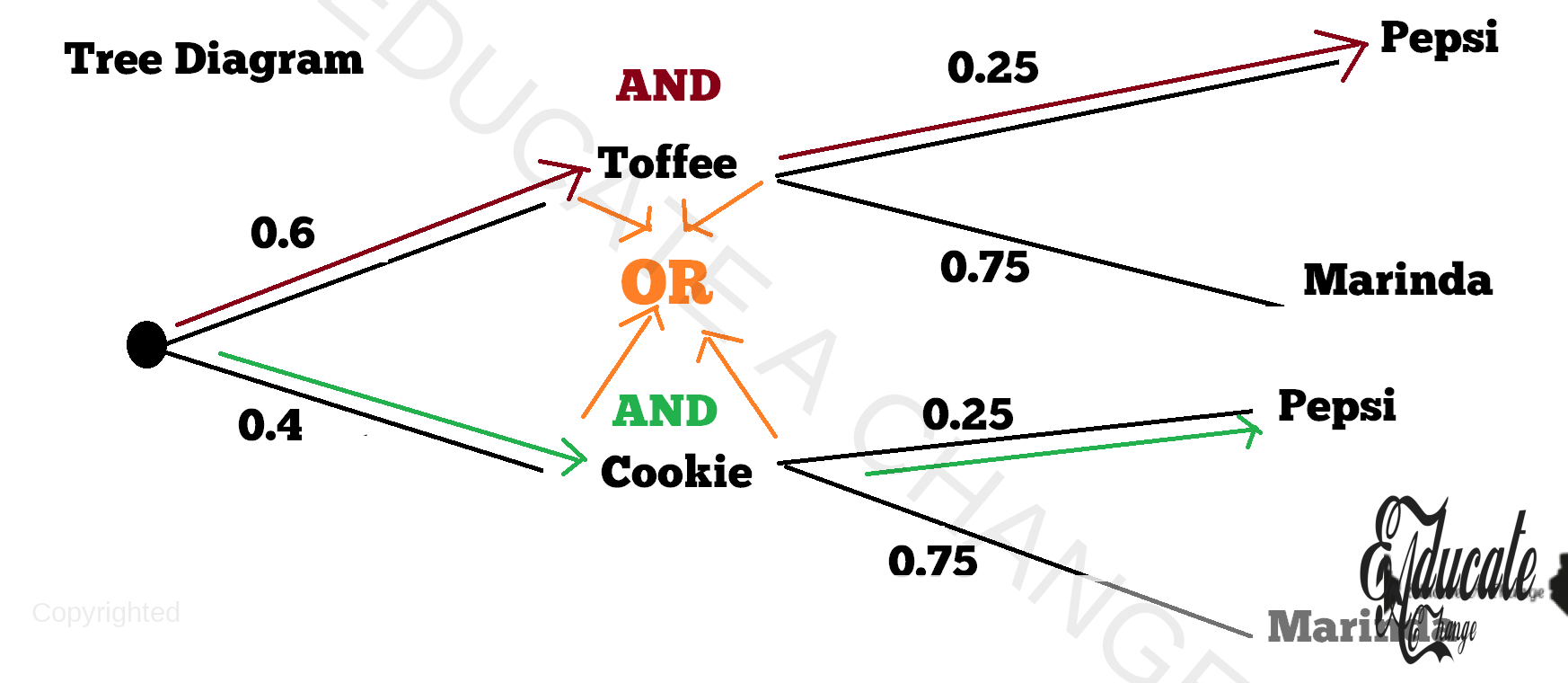
The use of And and Or Operators in Tree Diagrams

• In simple terms, when you go directly on the branches, it is an AND so we multiply.
• When we jump the branch completely, it is an OR so we add.
• Here are a few examples from our sample.
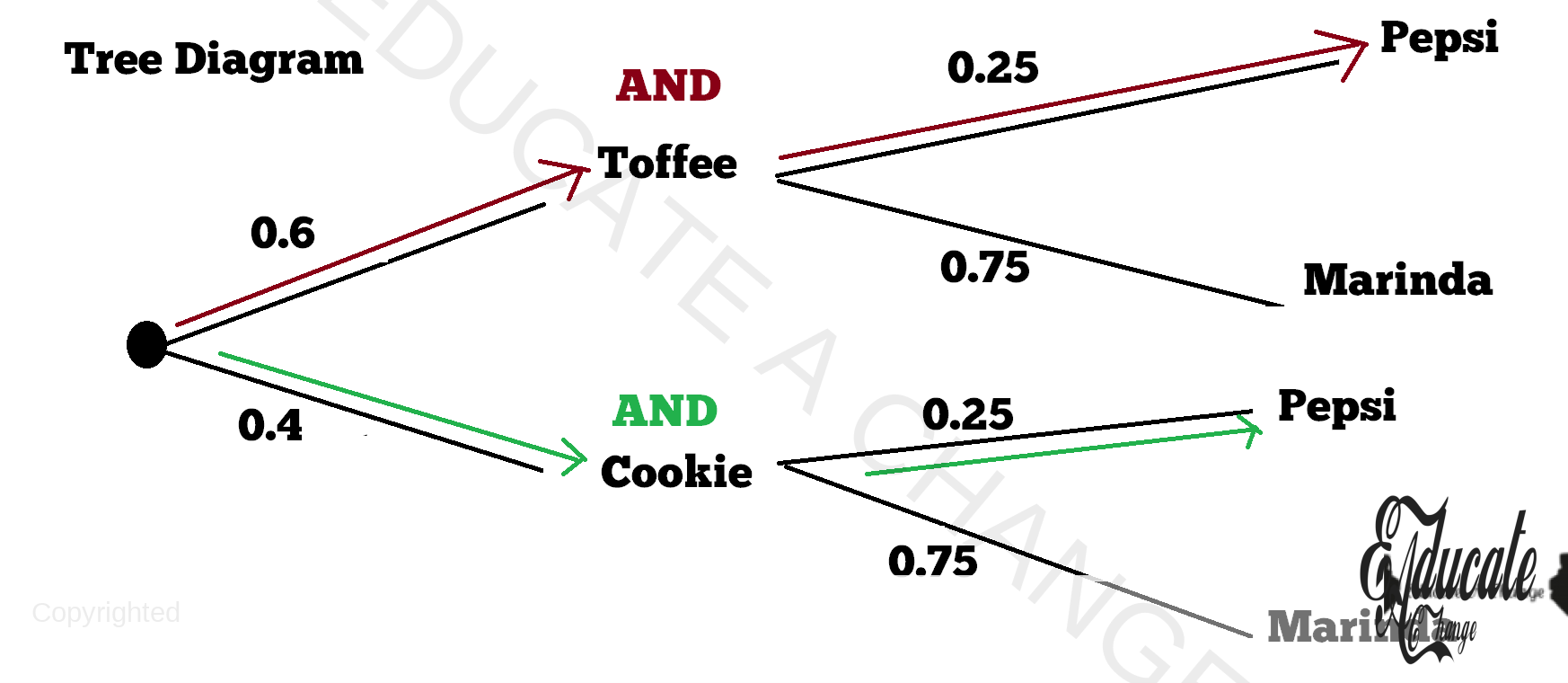
  • What would be the probability of selecting a toffee and Marinda

• Event A outcome Toffee: probability is 0.6
• Event B outcome Marinda: probability is
• We use the name branch, so we use AND
  • 6 AND 0.75
  • 6* 0.75 = 0.45
• Lets make it more complicated. Let say I will be happy if I either get Cookie and Pepsi or I get toffee and Pepsi.
  • As usual, let us break it down into simpler steps.
  • First branch: COOKIE AND PEPSI

• The probability of selecting Cookie is 0.4
• The probability of selecting Pepsi is 0.25
• Same branch so we use AND
• 4 AND 0.25
• 1

• Now let us consider about the second thing that will make me happy: Toffee and Pepsi.

• Again for this second scenario we will remain on the same branch.
• Probability to select a toffee is 0.6
• Probability to select Pepsi is 0.25
• I need both toffee AND Pepsi to be happy.
• 6 AND 0.25
• 6*0.25
• 15

• Now comes the interesting part. I am fine with EITHER scenario A (Cookie and Pepsi) being fulfilled completely OR scenario B (Toffee and Pepsi) being fulfilled completely. The situation between these become

• So I want EITHER complete scenario A which has a probability of 0.1 OR complete scenario B which has a probability of 0.15
• So we have an OR operator
• 1 + 0.15
• 25 is the total probability of either getting complete scenario A (Cookie and Pepsi) or getting complete scenario B (Toffee and Pepsi).

Remember

• No matter how many different events are in the tree-diagram, you have to construct even new event as as branches.

Tree Diagram – Dependent Events

• We covered independent events in the previous post. In this post, we will cover dependent events OR simply put, events that are not independent.
  • These are events where the outcome of the first event will impact the outcome of the second event.
  • There are two main types
    • Where first event is directly linked to the second event as a repetition of the first event.
      • For example, taking two toffees from a bag at random, one after another, without replacement. It means the outcome of the first event will impact the second event both in the total number of toffees that remain and the total count of each type of toffees that remain.
    • The second type is where although the events are not directly replicated as above, they still impact choices.
      • Say, I have to work on two days a week: Monday and Thursday. If I work late on Monday, I will either work half time or quarter time on Thursday. My probability of working half time on Thursday in this case will be 4/5 and working quarter time on Thursday will be 1/5. However, if I do not work late on Monday, I will either work full time on Thursday or not work at all on Thursday. My probability to work full time on Thursday will be 1/4 in this case, while my probability to not work on Thursday will be 3/4 in this case. The chances that I work late on Monday are 0.2.
    • We will consider both these questions here in detail.

The Replication-Based Dependent Events

• These are events where the first event is repeated in the second event.
• So for example
  • I have to pick two toffees from a bag at random, one after another, without replacement (NOTE: IF WITH REPLACEMENT, THESE EVENTS WOULD BECOME INDEPENDENT- THINK ABOUT IT).
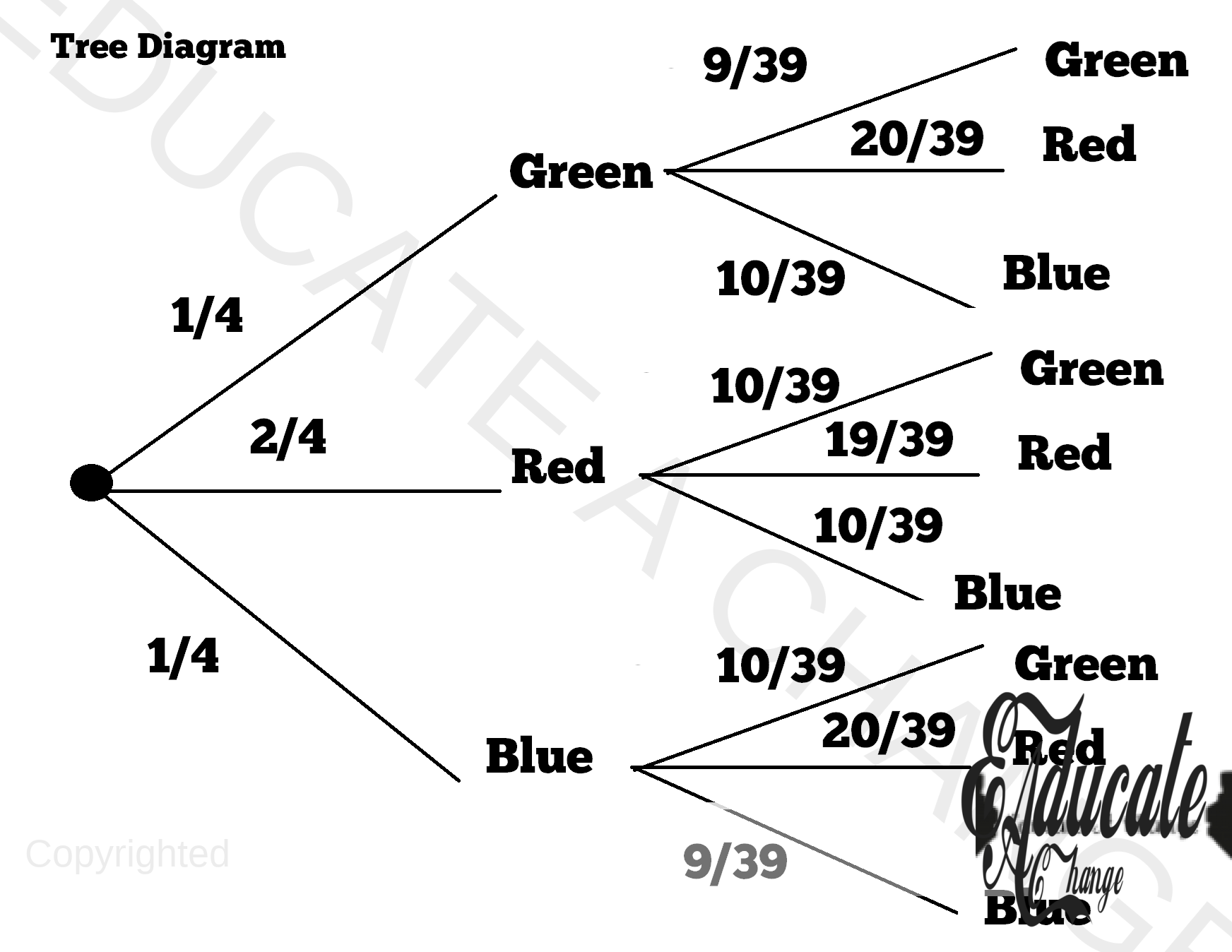
  • There are 40 toffees in the bag. 10 are green toffees, 20 are red toffees and 10 are blue toffees.
  • We will use fraction based probabilities here for clearer understanding.
  • So green toffees = 1/4, Red toffees = 2/4 and blue toffees = 1/4 are the probabilities.
• However, the second time I pick, the probabilities depend completely on my first choice. See the diagram below to understand.

• What happened here?
  • If I pick any toffee without replacement in the first pick, the total number in the bag falls from 40 to 39.
  • If I pick a green toffee in the first pick, the second pick would have ONE LESS GREEN toffee to pick from, reducing my total count to 9 GREEN toffees instead of 10.
  • If I pick a blue toffee in the first pick, the second pick would have ONE LESS BLUE toffee to pick from, reducing my total count to 9 BLUE toffees instead of 10.
  • If I pick a red toffee in the first pick, the second pick would have ONE LESS RED toffee to pick from, reducing my total count to 19 RED toffees instead of 20.
• Now, we can apply the same and and or rules as the situation might be as we discussed in the previous post for independent events. The real difference is in the construction of the tree diagram and the probabilities that go with it.

Complete Dependent Events

• The second type of dependent events is where the first choice completely changes your second choice.
• Here is a sample question that we will develop a tree diagram for. Do remember, the key to successfully attempting these questions is to break down the question into separate statements and develop a quick tree diagram to clarify what is actually being asked. First, let us consider how to break down a question:
• Question:
  • Say, I have to work on two days a week: Monday and Thursday. If I work late on Monday, I will either work half time or quarter time on Thursday. My probability of working half time on Thursday in this case will be 4/5 and working quarter time on Thursday will be 1/5. However, if I do not work late on Monday, I will either work full time on Thursday or not work at all on Thursday. My probability to work full time on Thursday will be 1/4 in this case, while my probability to not work on Thursday will be 3/4 in this case. The chances that I work late on Monday are 0.2.
  • DO NOT get confused in the question itself. Instead, think each independent event and its outcomes separately to make it simple for you. First, think of first event, its outcomes, then each second event and their outcomes. Do it step by step
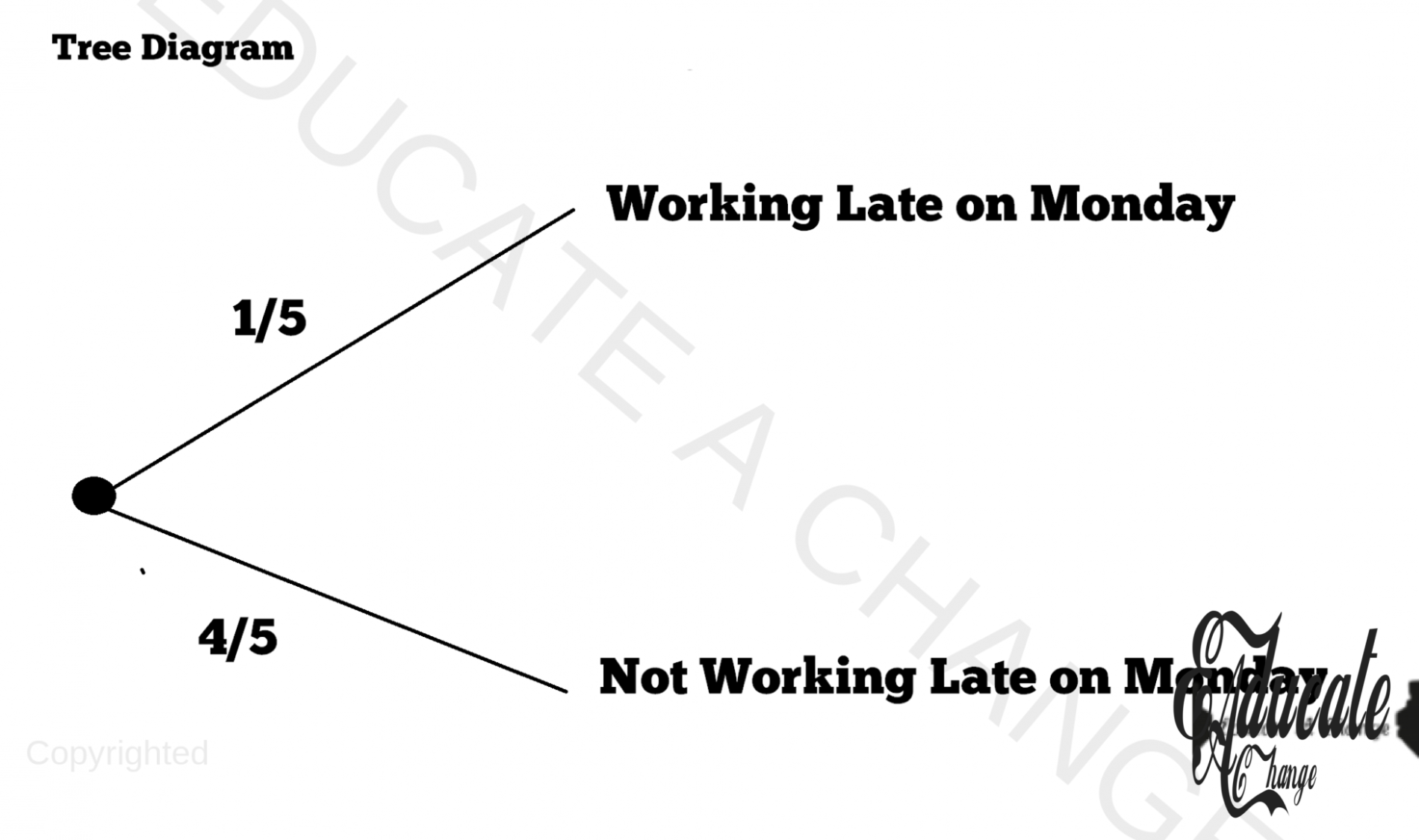
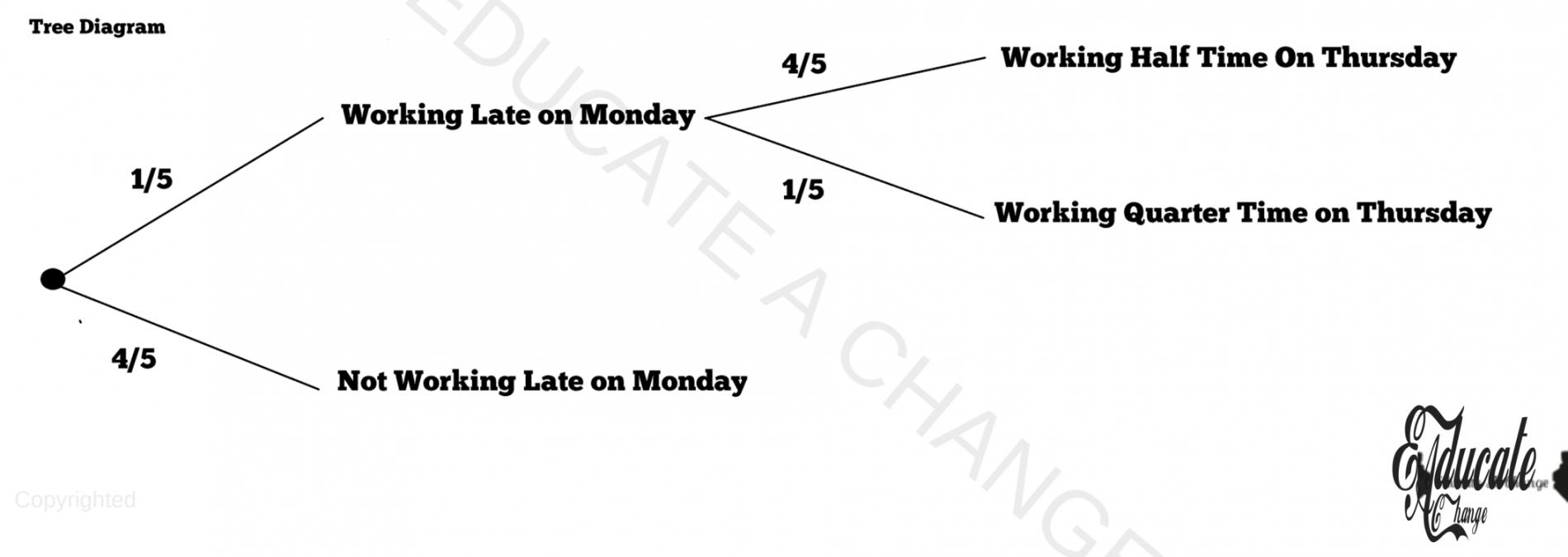
    • First let us decide what the first event is: How much I work on Monday. Now let us check its outcomes.
      • The two outcomes are, working late with a probability of 0.2 or 1/5.
      • The second outcome is not working late. Applying the 1- trick, we have 1-0.2 or 0.8 or 4/5 as the probability that I will not work late on Mondays. (1 is the maximum probability so we subtracted the first outcome’s probability from 1 to get the second outcome’s probability).
    • Now If I do work late, there are two outcomes of event B
      • I will either work half time on Thursdays with a probability of 4/5
      • Or I will work quarter time on Thursdays with 1/5 probability
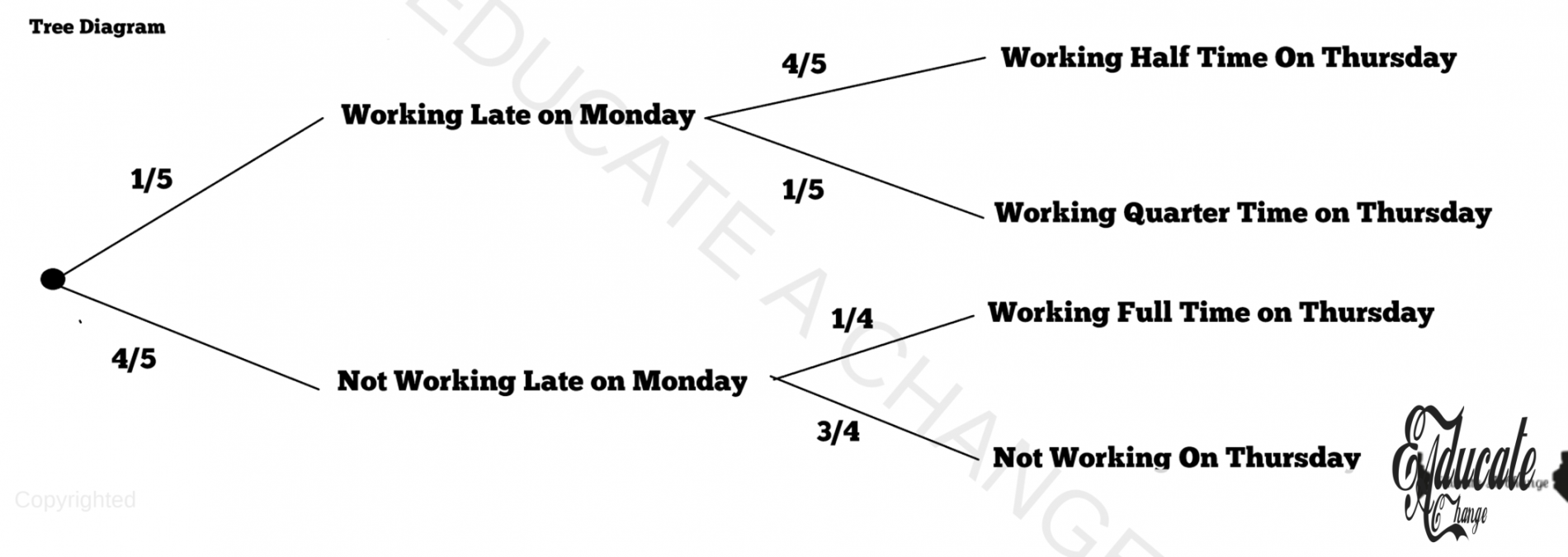
    • The second situation is that if I do not work late on Mondays, there are two outcomes of second event.
      • I will either work full time on Thursdays with 1/4 probability.
      • Or I will not work at all on Thursdays with 3/4 probability.
    • We have completely broken down the question. Now, let us use this information to make the tree diagram step by step.

Step 1: First Event

Step 2: Second Event Based On First Outcome of First Event

Step 3: Second Event Based On Second Outcome of First Event

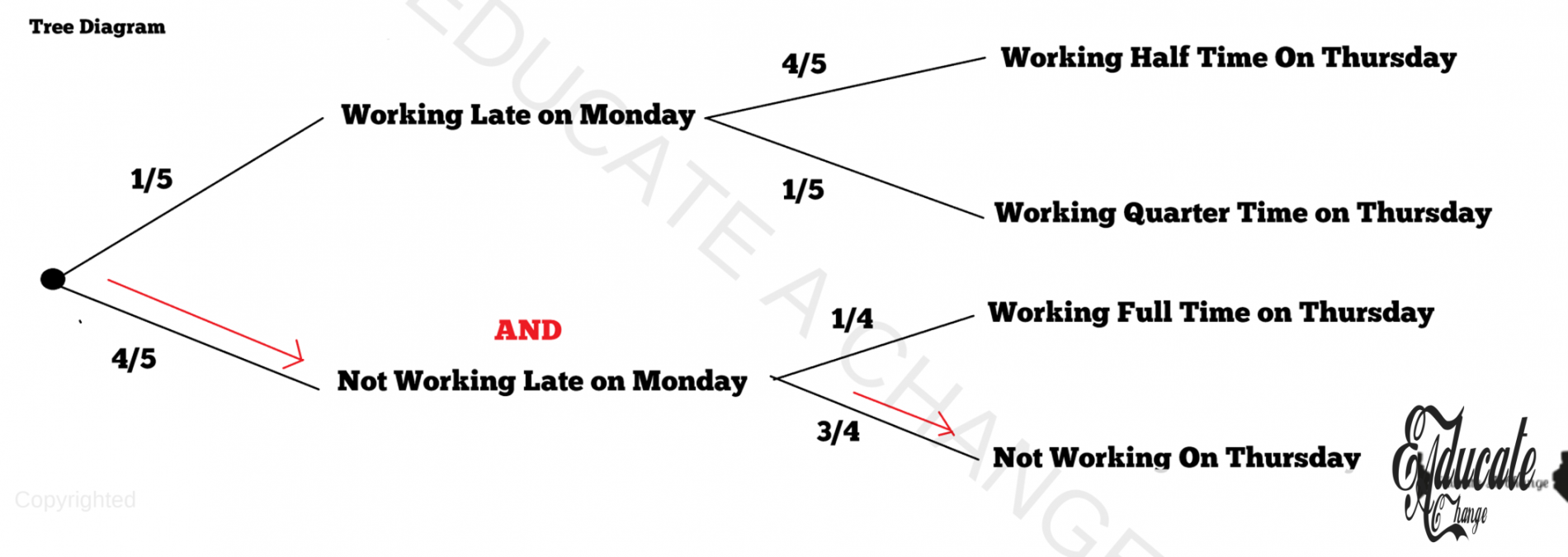
• The completes our tree diagram construction. Now, say, you need to find out the probability of not working late on Monday and not working at all on Thursday you will do the same as we discussed in the initial post

• So it would be 4/5 AND 3/4
• 4/5 * 3/4
• 12/20
• 3/5
• So we have a probability of 0.6 that I will not work late on Monday and not work at all on Thursday.

Possibility Diagrams

• A possibility diagram, as the name suggests, tells the possibility for something occurring. It is basically just writing down all possibilities in a diagram format and using it to calculate probabilities.
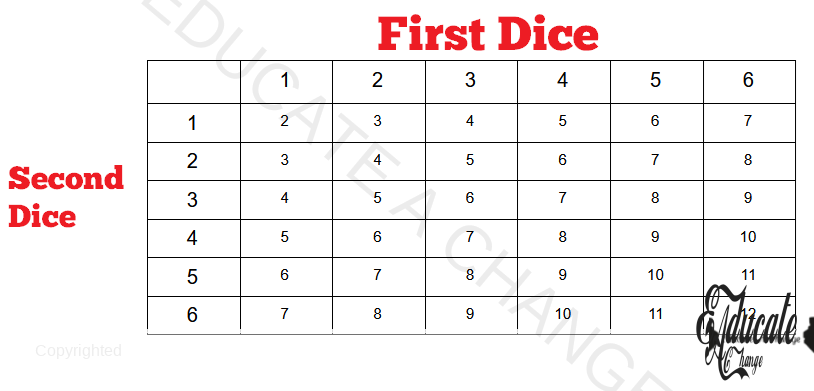
• For example, I have 2 regular 6-sided dice, with the number 1,2,3,4,5,6 on them. When I roll both dice together, what is the probability that the total score I get from both dice is, say, 8.
• We can construct a possibility diagram in this case:

• Now, it is easy for us to simply check that out of the total 36 possibilities, how many a total sums will be 8. Here, there are all the 8

• So we have a total of 5 out of 36 that are 8. That is 5/36 as the probability.

Probability Involving Sets

• It is actually very simple. (Do check our notes on Sets to understand how sets work in general)
• Let us say we have set A = {1,2,3,4,5,6}
• We have set B = {2,4,6,8,10}
• We know that the intersection set would be A∩B {2,4,6}
• Let us say he asks if a number is picked from set A, what is the probability that the number belongs to A∩B
• So, total numbers or elements in set A are 6. There are 3 numbers in set A that belong to the intersection set. So 3/6 probability. We can simplify it to 1/2.
• This is the basic thought behind set based probability.