Back

Trigonometry | O Level Mathematics 4024 & IGCSE Mathematics 0580 | Detailed Free Notes To Score An A Star (A*)

Views 0

The Basic Concept

  • Trigonometry comes from triangle
    • Basically right-angled triangle
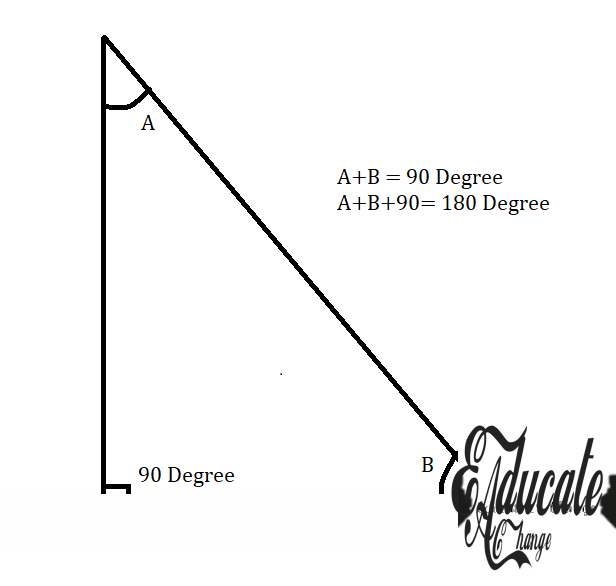
  • Any triangle has a total internal angle of 180°
    • So

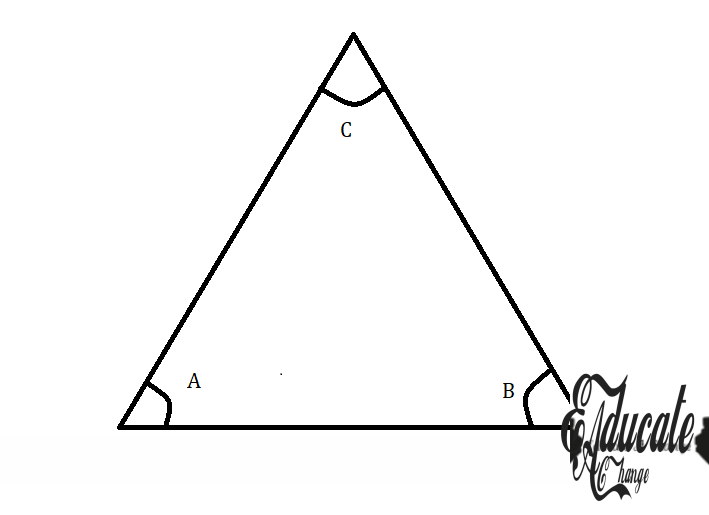
  • a+b+c = 180°
  • Remember
    • Small font for sides
    • Capital font for angles
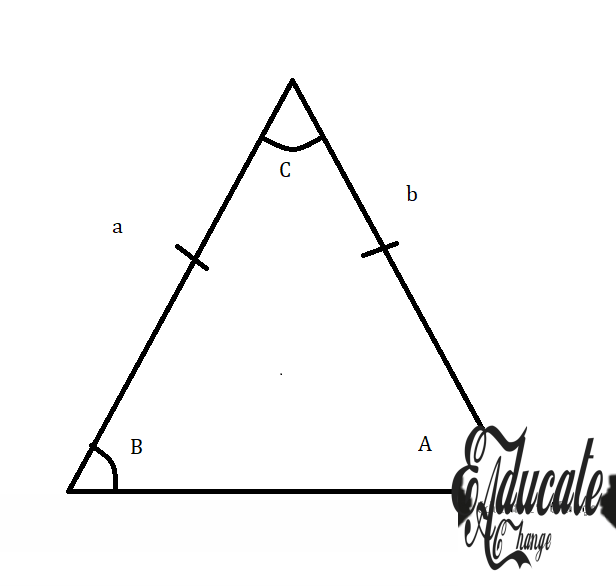
    • Corresponding angle / side
      • The side that is directly in front of an angle

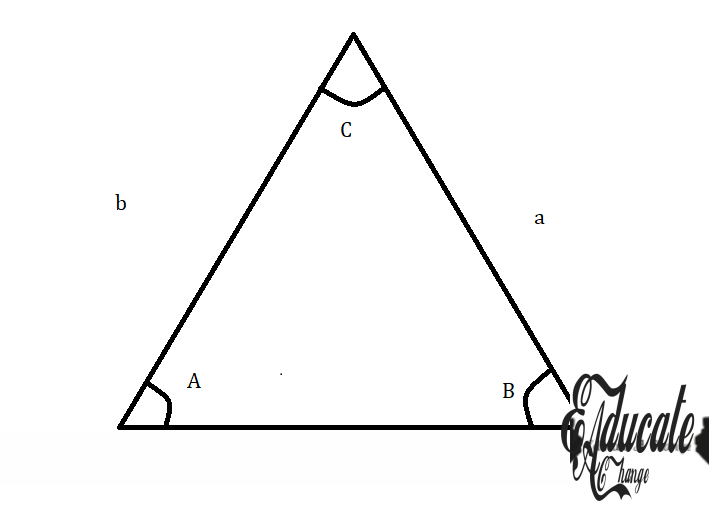
  • Remember one more thing
    • If you are given the term “Angle DZJ” it means the angle formed at Z
  • So in the above photo, angle A can be called Angle BAC or Angle CAB.
  • Angle B can be called Angle ABC or Angle CBA
  • Angle C can be called Angle ACB or Angle BCA
  • rightangled triangle
    • Will have 1 angle of 90 degree
    • The other two angles of less than 90 degree each
    • The total sum of the other 2 angles will be 90

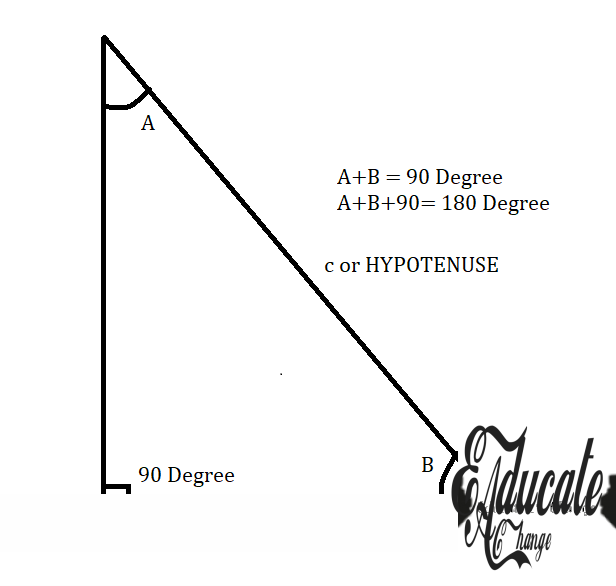
  • Here the sides are as followed
    • Hypotenuse will be constant
      • In the given diagram, only one side will be hypotenuse in any case
      • It will always be the corresponding side of 90 degree angle

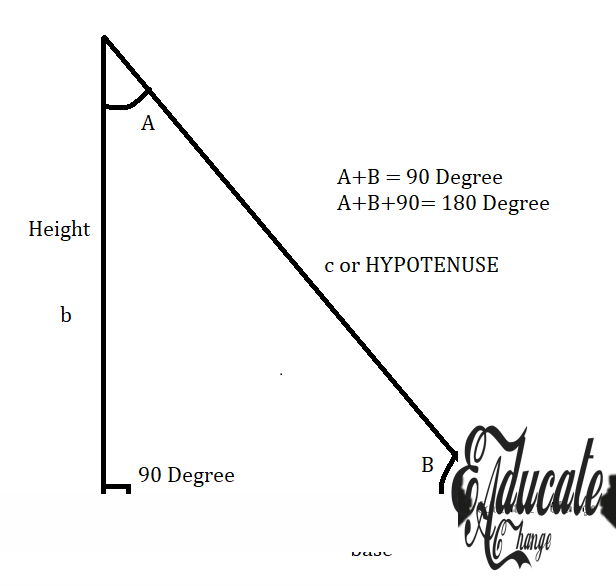
  • However
    • The base and height of the right angled triangle is RELATIVE to the angle you are considering
    • If you are considering angle B in the above diagram
    • Then side a will be base (the side in front of angle A)
    • The side b will be perpendicular height (the side in front of angle B)
    • So

  • However, if you consider angle A
    • Then base will be side b (The side in front of ANGLE B)
    • The perpendicular height will be the side a (The side in front of Angle A
  • This understanding is VERY IMPORTANT Because
    • Sin θ = height/hypotenuse
    • Cos θ = base/ hypotenuse
    • Tan θ = height / base
    • WHICH SIDE IS HEIGHT AND BASE
      • Will depend on the angle you are considering.
      • That is the key aspect here.
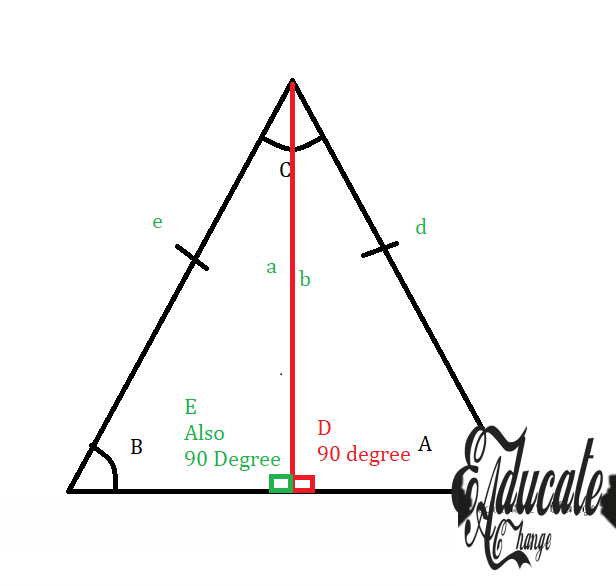
    • The second one is isosceles triangle
      • 2 angles and 2 sides are equal

  • Now after dividing in two parts, here is the new height and base etc.

  • So for the right angled triangle on the right
    • The three sides are a, d and half of c
    • The three angles are A, D and half of C
  • So for the right angled triangle on the left
    • The three sides are b, e and half of c
    • The three angles are B, E and half of C
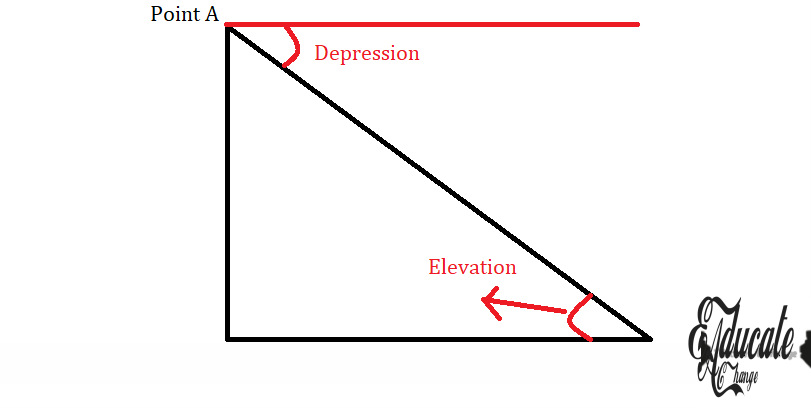
  • Angle of Elevation and Depression
    • Remember, for any given right angled triangle, THEY ARE THE SAME
      • Why?
        • Let us say it is the triangle I am considering

  • If I am standing at Point B and looking up at point A, the inner angle at point B and
    • The angle for the person who is standing at point A and looking down towards point B will be the exact same.
    • These angles are considered from eye level, meaning you have see where the eyes will go standing there
    • So

  • Both the angle and elevation from B to A and the angle of depression from A to B are the same
    • Remember, elevation is inner angle
    • Depression is outer angle
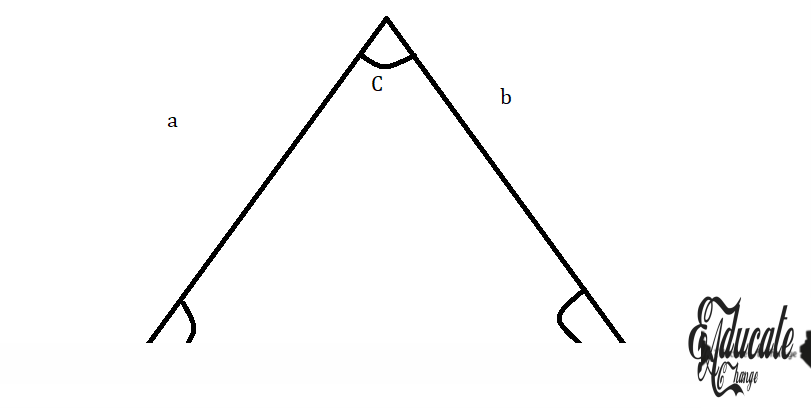
  • The Sine rule
    • You need the following MINIMUM requirements for sine rule
      • Any triangle not necessarily right angled triangle
      • You need one angle and its corresponding side
        • Apart from that you need either an angle or side
      • So

  • Here, we have enough requirements to find side b by sine rule
  • The rule is

  • Cosine Rule
    • We do not need a right angled triangle for this one as well
    • We need ANY triangle
    • We also need at least 2 sides and the included angle (the angle between those 2 side) as a minimum for this rule to apply

  • The rule is
    • a²= b²+c²- 2 (b) (c) Cos (A)
    • It can also be converted to
    • b² = a² + c² – 2 (a) (c) Cos (B)
    • And
    • c² = a² + b ² – 2 (a) (b) Cos (C)
  • Some guidance for PAPER 1
    • If we are considering this equation
      • a²= b²+c²- 2 (b) (c) Cos (A)
    • Then if you convert the equation to this form
      • (a²-b²-c²)/-2(b)(c) = Cost (A)
    • You have a few interesting aspects to consider
      • If
        • (a²-b²-c²)/-2(b)(c) gives you a NEGATIVE value
          • Then it is an obtuse angled triangle and the angle will be obtuse angle
        • If (a²-b²-c²)/-2(b)(c) gives you a positive answer
          • Then the angle is acute, but it does not confirm that the triangle is acute angled.
          • You need to check the other angles as well.
        • Remember
          • One triangle can have at a maximum ONE obtuse angle and it can never be a right angled triangle if one angle is obtuse
        • How to find angles if sides are given
          • For right angled triangle
            • You can use cos inverse, sin inverse and tan inverse
Hunain Zia

Hunain Zia has previously achieved considerable success in the high-school educational stream, gaining a massive 154 Total A Grades and 7 Major Distinctions, a process in which he broke/ set 11 different world records, including the most A grades ever achieved, most subjects ever appeared in, most distinctions, gaining distinctions across two separate boards (Pearson Edexcel and CAIE) within the same year/ ever, and even 19 hours of constant examination. All records stand intact today. Hunain pursued his Honors Accounting Degree from the prestigious Bentley University, and then completed an LLB (in Honors) from University of London. Currently, he manages multiple social and commercial projects, has founded digital streams and works tirelessly in the education sector.

Educate A Change focuses on truly bringing change in the educational sector worldwide. All our courses are designed to ensure success, and provide complete preparation without requiring any other external material. Therefore, it takes away the expense of academies, books, past paper compilations and other miscellaneous items. Instead, by just the courses we offer, the student can prepare fully for the best grades in their CAIEs, Edexcel and other high-school exams. The earnings from our course-sales are invested in social projects and growing the free educational activities of Educate A Change.