1.0 Lesson Objectives

• Circular Motion
  • Centripetal force
  • Applications
• Mass, Weight and Density
  • Mass and Weight
  • Inertia
  • Gravitational Field
  • Density
• Turning Effect of Forces
  • Moment
  • Center of Mass
  • Stability
• Deformation
  • Effect of Force on Shape and Size
  • Elastic objects
  • Hooke’s Law

1.1 Circular Motion:

So far, the main discussion has been on how objects move in straight paths. However, circular motion is also a very common movement that needs to be discussed in detail.

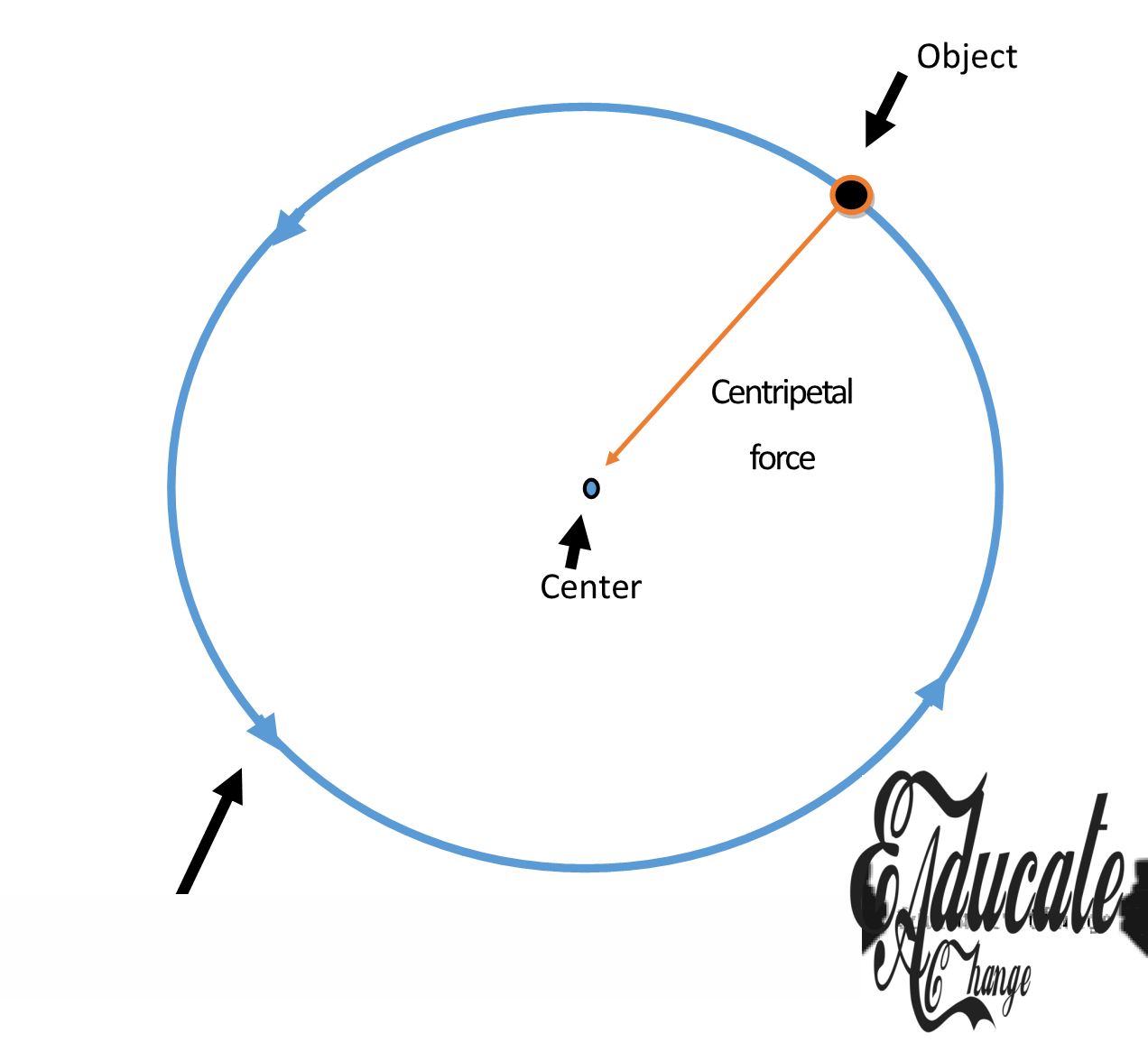
Centripetal Force:

• Circular motion is when objects move in a circular path. In order to keep a circular path, there must be a force acting on the object.
• This force is called the centripetal force and it’s the resultant force that always acts towards the center of the circle.
• If an object is moving in circular path, it can have constant speed, but its velocity is constantly changing in terms of direction and hence the object is accelerating. This means that there must be a resultant force constantly acting on the object. Hence, the centripetal force.

• Another reaction force acts away from the center called the centrifugal force; however, that discussion is beyond the scope of this syllabus.
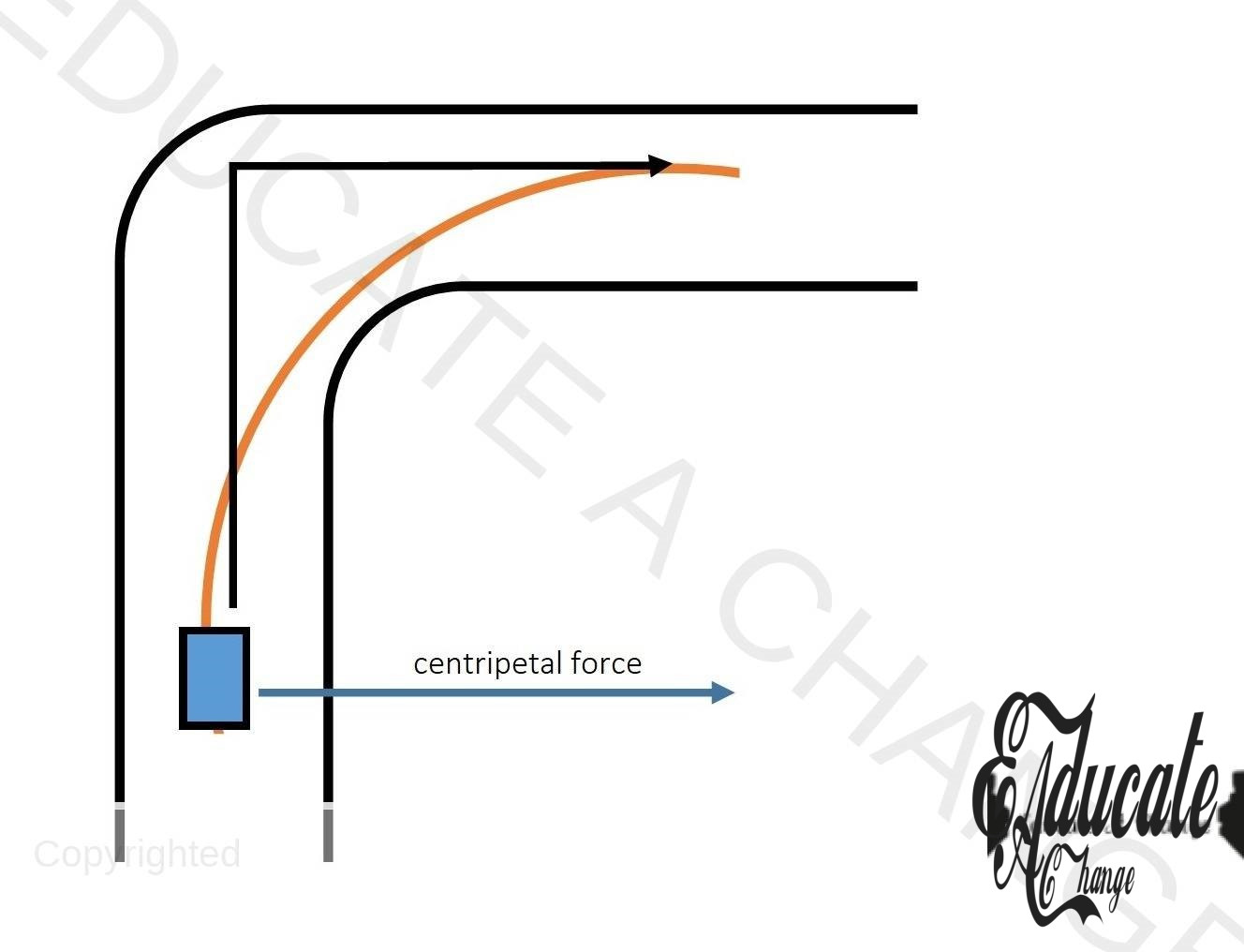
• We can consider a car moving around the corner. In that case, a circular path is being taken as well (red path), and hence the resultant force would be towards the center as depicted by blue arrow in the diagram.

1.2 Further Applications:

The same principle of circular motion can be applied to various different examples other than the car. Some common ones include:

• The motion of planets in the solar system
  • all the planets move in a circular motion around the sun and hence, they have a centripetal force that is acting towards the sun which keeps them in the orbit. If that force was removed, the planets would go off in a straight line forward.
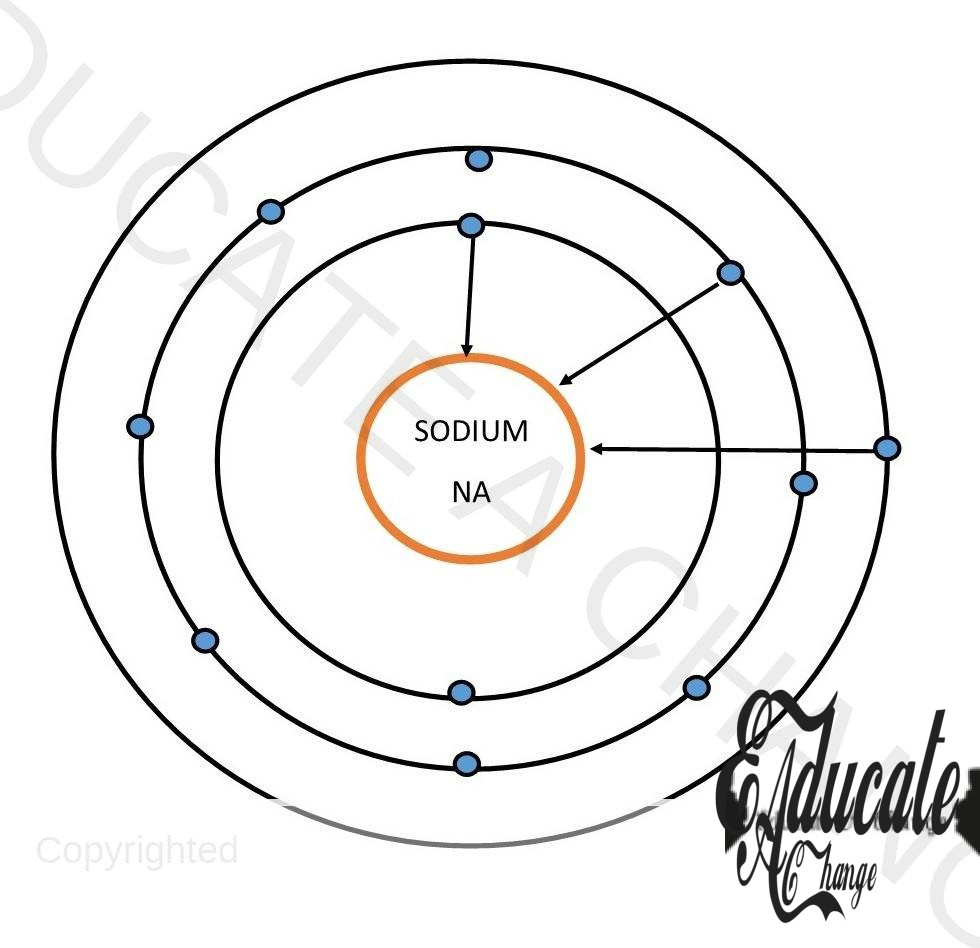
• The electrostatic forces of attraction of an atom’s nucleus to its electrons
  • The nucleus of an atom has electrostatic force of attraction towards the electrons in shells around the nucleus since the nucleus is positive in nature and electrons have a negative charge. This force acts as a centripetal force to keep the electrons in the circular shell.

• Gravitational forces on a satellite
  • Similar to the way planets move around sun, a satellite moves around earth due to the centripetal force caused by Earth’s gravitational pull. This keeps the satellites in orbit and prevent them from going away, out of their set loop.

1.3 Mass, Weight and Density:

Mass and Weight:

Mass:

Mass is the amount of matter a substance contains.

Weight:

Weight is the pull of gravity or in other words, the force exerted on objects due to the pull of gravity.

Differences between Mass and Weight:

Mass	Weight
Amount of substance	Pull of gravity
Measured by using beam balance/electronic balance	Measured by spring balance
Does not depend on the location	Depends on location
Scalar quantity	Vector quantity
SI UNIT: kilogram (kg)	SI UNIT: Newton (N)

 

Explanation:

• Mass does not change no matter what location we measure our mass in. This means if a man weights 50 kg on Earth, he will remain 50kg on Moon. However, since the weight is actually the force due to pull of gravity, and we know that Moon’s gravitational pull is less than Earth’s, hence a man will weigh more on Earth than on the Moon. So, weight is location dependent.
• Mass only has a magnitude since it is scalar. We cannot attach a direction to mass. However, weight has a direction which is towards the center of Earth.

1.4 Inertia:

• Inertia is a property of mass to resist the change in its state, either of rest or of motion.
• Since it is the property of mass, it depends on mass as well.
• This means that the more the mass, the more inertia a body will have. Mass and inertia are directly proportional.
• In order to understand inertia, we can consider the example of applying brakes. Consider, sitting in a car on a highway that is in constant motion. Suddenly, a huge truck comes in front and the driver immediately applies the brakes. What do you notice? Your body will move forward even though the car has stopped moving. This is due to inertia. Your body was in motion state and it is resisting the change in the motion state. Similarly, if we start the car again, and turn left, our body will move right, since we were going in a straight direction and now inertia prevents us from turning immediately to the left.

1.5 Gravitational Field:

Gravitational field is a region in which a mass experiences a force due to gravitational attraction. This force is the weight and since weight is a force, it causes an acceleration towards Earth which we have already studied in the terms of acceleration of free fall. Hence, the acceleration due to gravity is 9.8 m/s² on Earth. (approx. 10 m/s²). We know that Newton’s third law proves the formula: Force = mass x acceleration And we also know that weight causes the acceleration due to gravity which is 9.8, then the formula changes to : Weight = mass x 9.81 For all objects near Earth’s surface. However, we have to generate a generic formula that can be applied anywhere so if we call the gravitational acceleration to be ‘g’, our formula becomes: W = mg: standard Formula for weight.

1.6 Density:

• Density can be defined as the mass per unit volume of a substance. Density defines how close the particles are in a substance or how much mass is present in a unit volume of a substance.
• If we take two similar sized bags and fill a bag with rice till there is no more space, and on the other hand we fill a bag with cement till no space is left, we will see that the bag of rice will be lighter as compared to the bag of cement even though both fillings were in the same volume. This is because a bag of rice is less dense as compared to a bag of cement. When we weigh both bags, the bag of rice will have a much lower mass as compared to the bag of cement.
• On the contrary, if we fill a bag with 20kg rice and other with 20kg cement, both our bags will have the same mass (20kg) but the bag of rice will look more filled as compared to the bag of cement since cement is denser than rice and require less volume for 20kg.
• If we discuss the density of water, we can understand that the objects that have less density than water, float and the objects will more density than water sink.

1.7 Calculating Density:

• Since density is mass per unit volume, we can write it as
  • Density = mass / volume
• We commonly use the symbol ρ to write density. The unit of density is kg/m³ or g/cm³.
• In order to calculate density:
  • we can measure mass using beam balance or electronic balance.
  • Volume:
    • For liquids, simple use a measuring cylinder to measure volume,
    • For regular shapes, volume calculation is simpler by the use of formulas such as for a cubic shape.
    • For irregular shapes, we take a fixed volume of water, and immerse our object into the water. By taking a new volume, we can subtract the original volume of water an find out the volume occupied by the object.
    • If our object floats on water, we can attach it to a heavier object and take the volume reading when our object is under the water with the heavy object and subtract the reading of just the heavy object in water from it.
  • Finally, we divide the mass with volume and find our density.
• Remember, density does not depend on the shape of the object, it depends on the material. If we were to cut out various different shapes of objects from a same sheet of metal, they will all have the same density!

1.8 Turning Effects of Forces:

Moment:

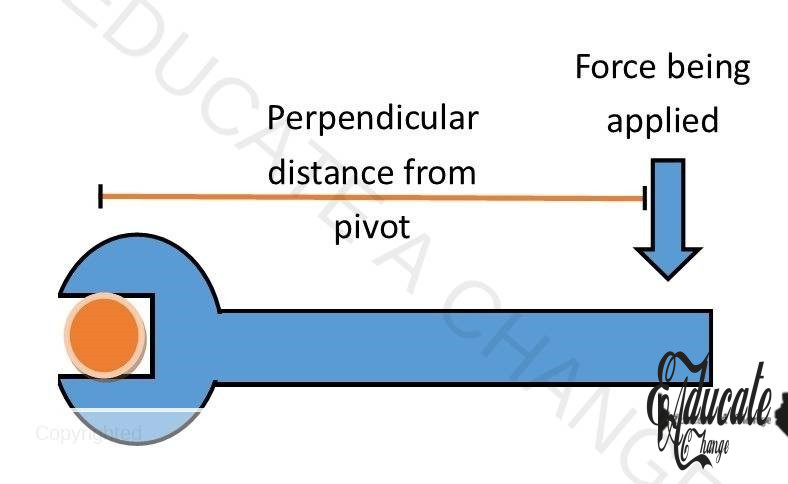
• Moment is the turning effect of force.
• Moment can be defined as the product of force applied and the perpendicular distance between the force and the pivot.
• SI Unit of moment is Newton Meters or Nm.
• As illustrated in the diagram, the pivot is the central point which is the nut and the wrench is where the force is being applied.

• Moment is directly proportional to force and to the distance. As we decrease the distance, moment decreases and similarly, as we decrease the force applied, there is less moment.
  • For this reason, using a longer spanner will make tightening nuts easier than a short spanner.
• Since moment is created by perpendicular distance, if the angle is 90 degrees, the moment will be the highest. Decreasing the angle between the force and pivot will decrease the moment.

Examples:

• When we use a wrench to turn a nut, the force we apply on the wrench is creating a moment.
• In parks, the seesaws are a very good example of turning effect of forces where there is a central point of the swing and the weight of the children create a turning effect.

Principle of Moment:

• The principle of moment state that when an object is in equilibrium, the total anticlockwise moment is equal to the total clockwise moment.
• Sum of anticlockwise moment = Sum of clockwise moment

 

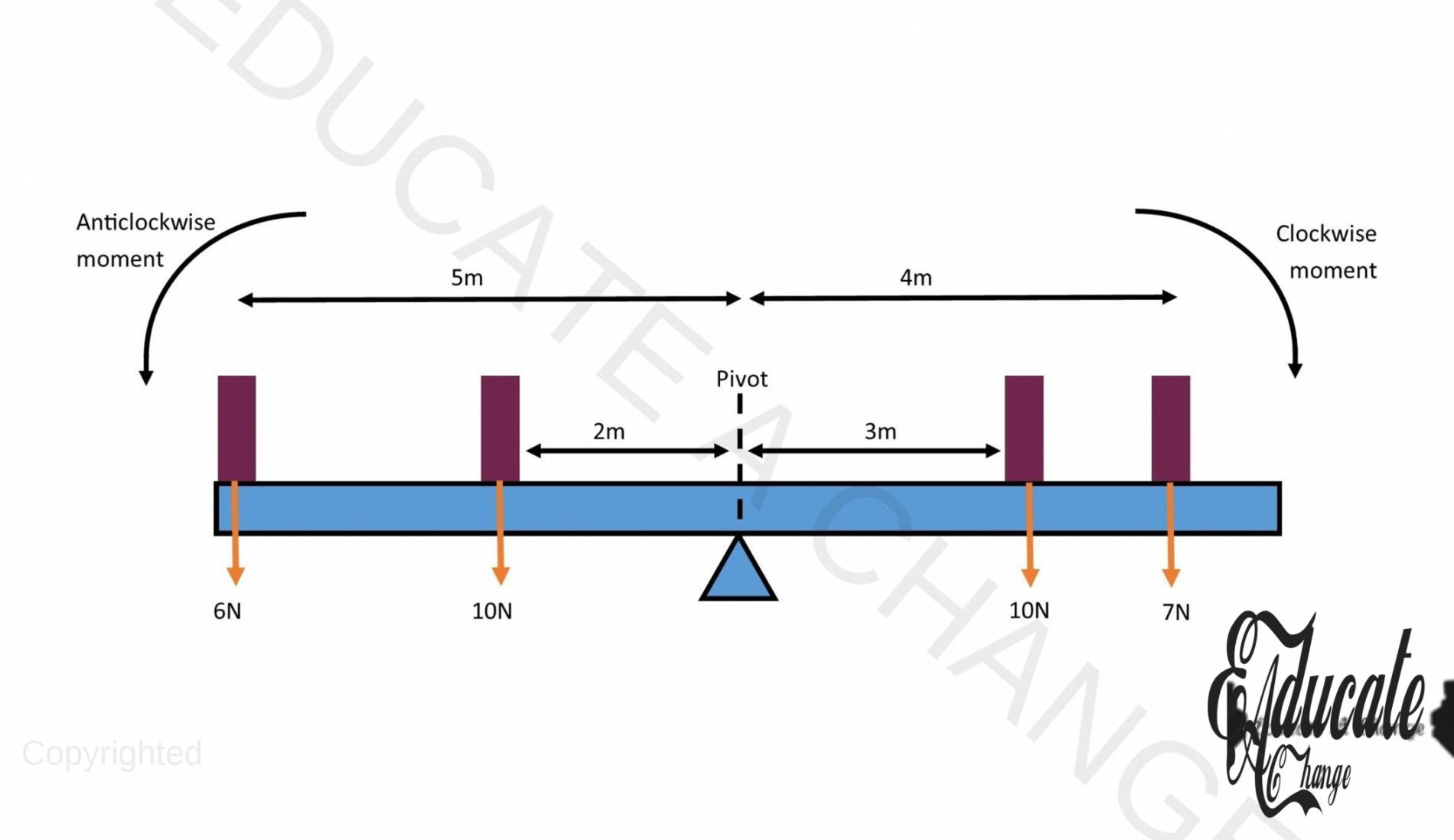
Example Calculation:

For example, consider this diagram of a swing. We place for blocks at four places on the swing, each with a different weight. Now we shall calculate whether the swing is in equilibrium or not.

• As we can see, the blocks to the left of the swing will create an anticlockwise moment and the blocks to the right of the swing shall create a clockwise moment. We shall first calculate both sides of the moment in order to find the final moment on the swing.
• Anticlockwise moments:
  • Moment= force x distance = 5m x 6N + 2m x 10N = 30Nm + 20Nm = 50Nm anticlockwise moment.
• Clockwise moments:
  • Moment= force x distance = 3m x 10N + 4m x 7N = 30Nm +28Nm = 58Nm clockwise moment.
• This means that since there is an 8Nm extra moment on the right side of the swing, the swing shall move in the clockwise direction as 58Nm – 50Nm = 8Nm extra moment clockwise.
• If we are to balance a swing by adding another weight, we have to add that weight to the left side of the swing in a way that it increases the anticlockwise moment by 8Nm.
• For example, we have an extra weight of 4N. We can add that to the swing at a distance of 2m since:
  • Moment = force x distance, 8Nm = 4N x Y = Y distance = 2m from the pivot
• So, if we are to add that 4N weight ,2 meters left from the pivot, our swing will become balanced.
• We can verify the principle of moment after the swing is balanced by calculating the clockwise and anticlockwise moments which now turn out to be equal for a balanced swing.

1.9 Center of Mass and Gravity:

The center of gravity of an object is the point at which the entire weight of the object seems to be concentrated. Similarly, the center of mass is the point where the entire mass of an object seems to be concentrated. Under normal conditions, the center of gravity and the center of mass are the same.

Calculating Center of Gravity:

There are two cases that need to be discussed:

• Regular Objects:
  • In case the shape of an object is regular, then the center of gravity is the geometrical center of the object.
• Irregular Objects: Plain Lamina:
  • When discussing plain objects, the discuss finding the center of gravity of plain lamina or plain surface. In order to calculate the center of gravity:
    • Make three holes, near the edges of the lamina.
    • The holes should be as far apart from each other as possible.
    • Hang the lamina using a pin through one of the holes.
    • Hang a plumb line (a weighted bob) in front of the lamina.
    • When the plumb line becomes stable, draw a line over the lamina.
    • Repeat the procedure through the other two holes.
    • The point of intersection of the three lines is the center of gravity of the plain lamina.

 

2.0 Stability:

Stability of an object depicts how likely it is for an object to return to its original state when it is slightly changed. For example, if we push a glass from the top, for a certain amount of push, the glass will return to its original standing state. After a certain amount of force, the glass will topple over. This is the stability of the glass.

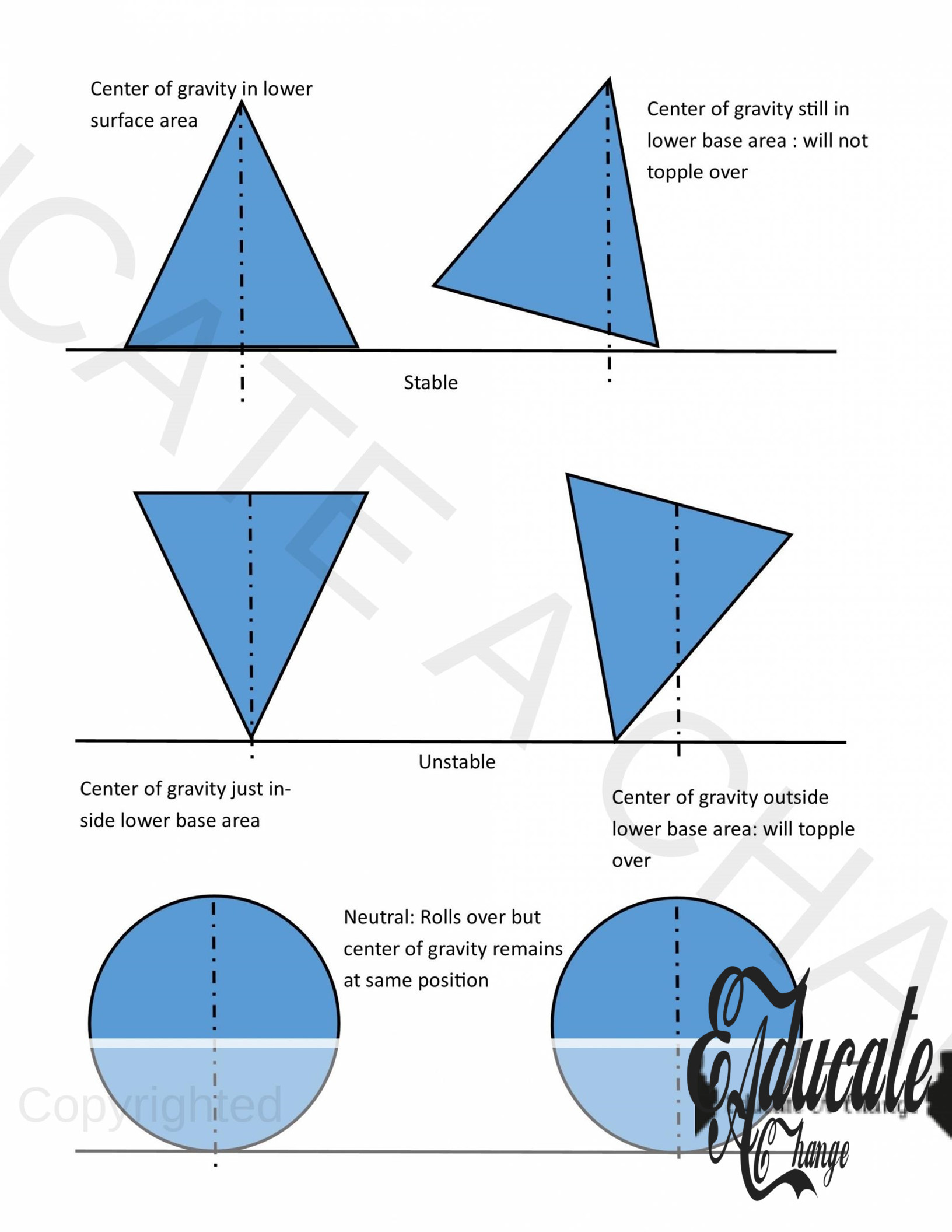
States of Equilibrium:

There are three states of equilibrium:

• Stable
  • The object has a tendency to return to its state when its slightly nudged. This happens if after the object is displaced, the center of gravity still passes its base area. In that case, the object shall return to its original state
• Unstable
  • The object shall change state any moment its left unattended and won’t return to original position. This happens when the center of gravity lies outside the base area.
• Neutral
  • When an object will change position with slight displacement, but its center of gravity remains the same, then the object is said to be in neutral equilibrium

Increasing Stability:

• Stability of an object depends on two major factors: The base area and the center of gravity
  • Lowering the center of gravity will make objects more stable
  • Increasing the base area will make objects more stable.

2.1 Deformation:

Effect of Force on Shape and Size:

As we already discussed in Dynamics, Force can have several effects on an object. It can change an objects speed and direction. Another effect that force can have on an object is to change an object’s shape and size. The larger the applied force is, the greater the change in shape and size shall be for objects that can change.

2.2 Elastic Objects:

• Objects that restore their original size and shape, once a force being applied is removed, are known as elastic objects. An elastic material can be compressed, stretched and twisted.
• For example, a rubber band or a spring can be extended to increase in size and change its shape. However, once the force being applied is removed, they return to their original shape.

 

2.3 Hooke’s Law:

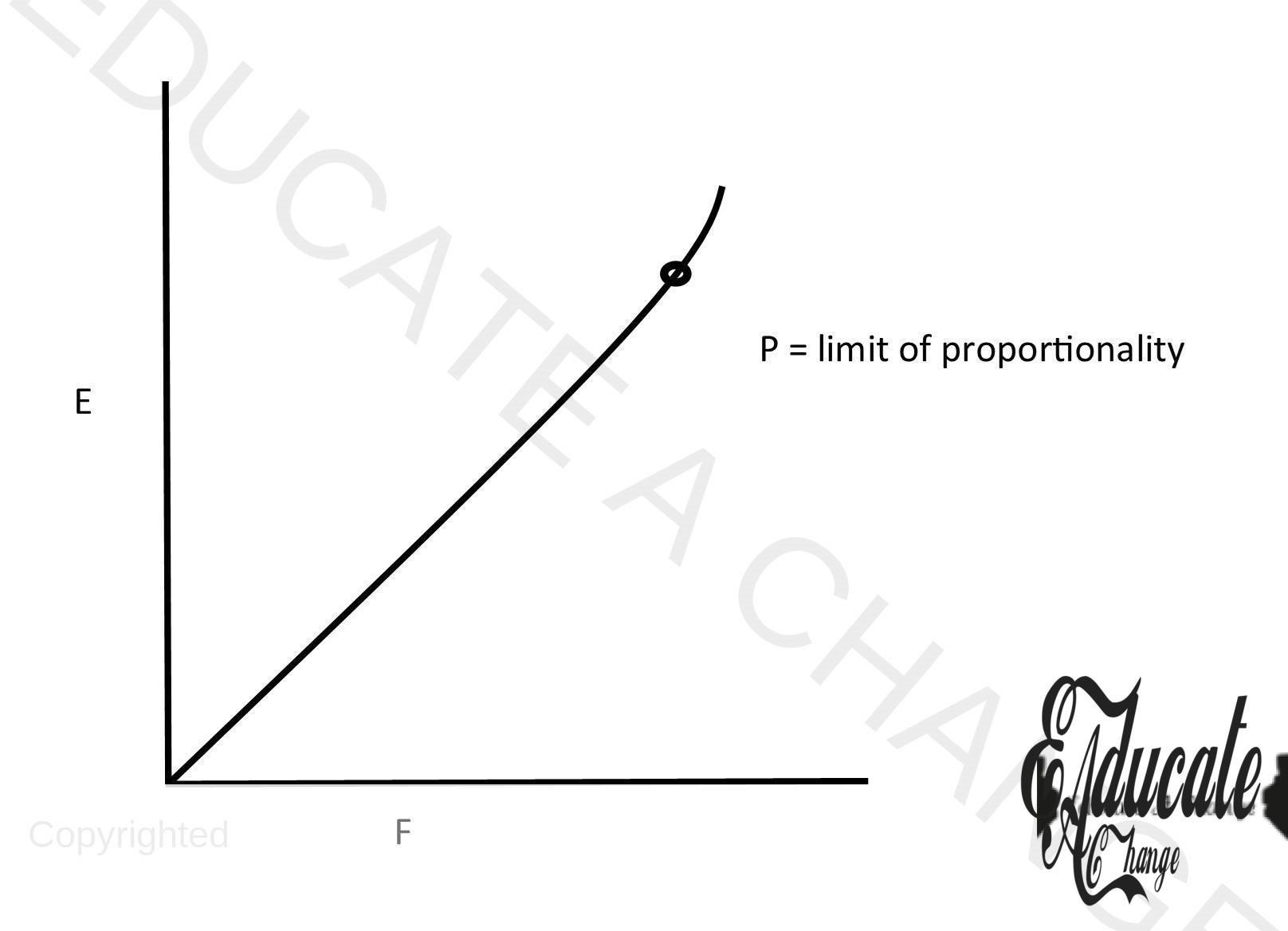
• Hooke’s Law states that when an elastic object is stretched, the stretching force is proportional to the extension of an object, provided that stretching force is not great enough that it deforms the object permanently or the limit of proportionality is reached.
• Force ∝ extension until limit of proportionality

Limit of Proportionality:

The limit after which Hooke’s law is no longer applicable and an object cannot return to its original length.

Spring Constant:

• K (spring constant) depends on the nature of the material.
• F ∝ E
• F = KE

Calculating Spring Constant:

In order to find the spring constant of an object, we can place a spring in front of a rule and measure its initial length. Then by applying a specific weight to it, we can measure the new length and using the formula F = KE, we can calculate the value of K. However, we need to make sure, not to extend the spring beyond its limit of proportionality.